Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 77 Vở thực hành Toán 7. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
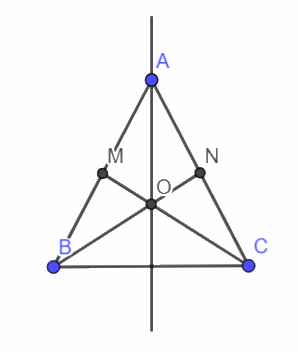
Bài 5. Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm AB, AC. Gọi O là giao diểm của đường thẳng BN và CM. Chứng minh rằng O nằm trên đường trung trực của đoạn thẳng BC.
Đề bài
Bài 5. Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm AB, AC. Gọi O là giao diểm của đường thẳng BN và CM. Chứng minh rằng O nằm trên đường trung trực của đoạn thẳng BC.
Phương pháp giải - Xem chi tiết
Chứng minh OB = OC
Lời giải chi tiết
GT | \(\Delta ABC\)cân tại A,\(M \in AC,N \in AC,AM = MB,\) \(AN = NC,BN \cap CM = O.\) |
KL | O thuộc trung trực BC |
Hai tam giác ABN và ACM có:
AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat {BAN} = \widehat {CAM}\)(góc chung)
\(AN = \frac{{AC}}{2} = \frac{{AB}}{2} = AM\)(\(\Delta ABC\)cân tại A)
Vậy \(\Delta ABN = \Delta ACM\)(c-g-c). Từ đó suy ra \(\widehat {ABN} = \widehat {ACM},\widehat {ANB} = \widehat {AMC}\)
Hai tam giác BOM và CON có:
\(\widehat {OMB} = {180^o} - \widehat {AMC} = {180^o} - \widehat {ANB} = \widehat {ONC}\)(chứng minh trên)
\(BM = \frac{{AB}}{2} = \frac{{AC}}{2} = CN\)(\(\Delta ABC\)cân tại A)
\(\widehat {MBO} = \widehat {ABN} = \widehat {ACM} = \widehat {NCO}\)(chứng minh trên)
Vậy \(\Delta BOM = \Delta CON\)(g-c-g). Do đó OB = OC.
Vậy O cách đều hai đầu của đoạn thẳng BC. Suy ra O nằm trên trung trực của BC.
Bài 5 trang 77 Vở thực hành Toán 7 thuộc chương trình học Toán lớp 7, thường liên quan đến các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của các phép toán này. Việc nắm vững kiến thức nền tảng là điều kiện tiên quyết để giải quyết bài tập một cách chính xác và hiệu quả.
Bài 5 trang 77 thường bao gồm các dạng bài tập sau:
Để giải bài tập bài 5 trang 77 Vở thực hành Toán 7 một cách hiệu quả, các em có thể áp dụng các phương pháp sau:
Ví dụ 1: Tính giá trị của biểu thức sau: (1/2) + (2/3) - (1/6)
Giải:
(1/2) + (2/3) - (1/6) = (3/6) + (4/6) - (1/6) = (3 + 4 - 1)/6 = 6/6 = 1
Ví dụ 2: Tìm x biết: x + (1/3) = (5/6)
Giải:
x = (5/6) - (1/3) = (5/6) - (2/6) = 3/6 = 1/2
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tự giải thêm các bài tập tương tự trong Vở thực hành Toán 7, hoặc tham khảo các tài liệu học tập khác.
Học Toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Các em nên dành thời gian ôn tập kiến thức, làm bài tập, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt!
| Phép toán | Công thức |
|---|---|
| Cộng | a/b + c/d = (ad + bc) / bd |
| Trừ | a/b - c/d = (ad - bc) / bd |
| Nhân | (a/b) * (c/d) = (ac) / (bd) |
| Chia | (a/b) : (c/d) = (a/b) * (d/c) = (ad) / (bc) |