Bài 5 (7.34) trang 47, 48 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số hữu tỉ, đặc biệt là các bài toán liên quan đến phân số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 (7.34) trang 47, 48 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: (Fleft( x right) = Gleft( x right).Qleft( x right) + Rleft( x right)). a) (Fleft( x right) = 6{x^4} - 3{x^3} + 15{x^2} + 2x - 1;Gleft( x right) = 3{x^2}). b) (Fleft( x right) = 12{x^4} + 10{x^3} - x - 3;Gleft( x right) = 3{x^2} + x + 1).
Đề bài
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: \(F\left( x \right) = G\left( x \right).Q\left( x \right) + R\left( x \right)\).
a) \(F\left( x \right) = 6{x^4} - 3{x^3} + 15{x^2} + 2x - 1;G\left( x \right) = 3{x^2}\).
b) \(F\left( x \right) = 12{x^4} + 10{x^3} - x - 3;G\left( x \right) = 3{x^2} + x + 1\).
Phương pháp giải - Xem chi tiết
Khi chia đa thức A cho đa thức B ta được đa thức thương là Q, đa thức dư là R, ta luôn có đẳng thức: \(A = BQ + R\).
Lời giải chi tiết
a) Ta có:
\(\left( {6{x^4} - 3{x^3} + 15{x^2} + 2x - 1} \right):3{x^2} = 2{x^2} - x + 5\) (dư \(2x - 1\))
Vậy \(F\left( x \right) = G\left( x \right).\left( {2{x^2} - x + 5} \right) + 2x - 1\).
b) Đặt tính chia:
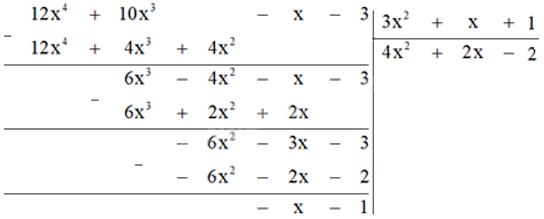
Vậy \(F\left( x \right) = G\left( x \right).\left( {4{x^2} + 2x - 2} \right) - x - 1\)
Bài 5 (7.34) trang 47, 48 Vở thực hành Toán 7 tập 2 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ. Để giải bài tập này, các em cần nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ, cũng như quy tắc chuyển đổi phân số về dạng tối giản.
Phần a của bài tập yêu cầu tính các biểu thức sau:
Để giải các biểu thức này, ta thực hiện theo thứ tự các phép toán trong ngoặc trước, sau đó đến phép nhân, chia, cộng, trừ.
Phần b của bài tập yêu cầu tìm x trong các phương trình sau:
Để giải các phương trình này, ta sử dụng các quy tắc chuyển vế và các phép toán ngược.
Khi giải bài tập về số hữu tỉ, các em cần chú ý:
Bài 5 (7.34) trang 47, 48 Vở thực hành Toán 7 tập 2 là một bài tập cơ bản nhưng quan trọng. Việc nắm vững các quy tắc và kỹ năng giải bài tập này sẽ giúp các em học sinh tự tin hơn trong việc học Toán 7.