Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 9 Vở thực hành Toán 7. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
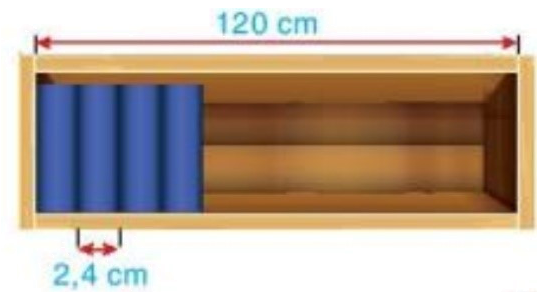
Ngăn đựng sách của một giá sách trong thư viện dài 120 cm (xem hình bên). Người ta dự định xếp các cuốn sách dày khoảng 2,4 cm vào ngăn này. Hỏi ngăn sách đó có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?
Đề bài
Ngăn đựng sách của một giá sách trong thư viện dài 120 cm (xem hình bên). Người ta dự định xếp các cuốn sách dày khoảng 2,4 cm vào ngăn này. Hỏi ngăn sách đó có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?
Phương pháp giải - Xem chi tiết
- Chiều dài ngắn sách là độ dài đoạn thẳng
- Độ dày cuốn sách là độ dài đoạn thẳng bị chia nhỏ
Lời giải chi tiết
Ngăn sách có thể đựng nhiều nhất số cuốn sách là:
\(\begin{array}{l}120:2,4 = 120:\frac{{24}}{{10}}\\ = 120.\frac{{10}}{{24}} = \frac{{120.10}}{{24}} = 50\end{array}\)
Vậy số sách có thể đựng là 50 cuốn.
Bài 5 trang 9 Vở thực hành Toán 7 thường thuộc chương trình học về các phép toán cơ bản với số nguyên, số hữu tỉ, hoặc các bài toán liên quan đến lũy thừa. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức nền tảng và áp dụng đúng các quy tắc, tính chất toán học.
Để cung cấp một lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 5 trang 9 trong Vở thực hành Toán 7. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và các đề bài tương tự, chúng ta có thể phân tích các dạng bài tập thường gặp và cách giải:
Các bài tập thuộc dạng này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số nguyên, đồng thời áp dụng các quy tắc về thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau). Ví dụ:
Tính: a) 12 + (-5) b) (-8) - 3 c) 4 x (-2) d) (-15) : 5
Lời giải:
Khi làm việc với số hữu tỉ, học sinh cần chuyển đổi các số thập phân về phân số hoặc sử dụng máy tính bỏ túi để đảm bảo độ chính xác. Ví dụ:
Tính: a) 1/2 + 3/4 b) 2/5 - 1/3 c) 3/7 x 2/5 d) 4/9 : 1/2
Lời giải:
Học sinh cần nắm vững các quy tắc về lũy thừa, bao gồm lũy thừa bậc hai, lũy thừa bậc ba, và các tính chất của lũy thừa. Ví dụ:
Tính: a) 23 b) (-3)2 c) (1/2)2 d) 50
Lời giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh đã có thể tự tin giải bài 5 trang 9 Vở thực hành Toán 7. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!