Bài 4 (9.39) trang 88 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 (9.39) trang 88 VTH Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho (BD = 2DC). Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.47). Chứng minh rằng tam giác ABE cân tại A. Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến.
Đề bài
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho \(BD = 2DC\). Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.47). Chứng minh rằng tam giác ABE cân tại A.
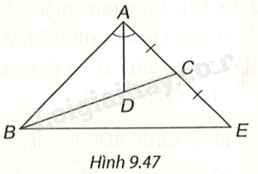
Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến.
Phương pháp giải - Xem chi tiết
+ Chứng minh D là trọng tâm tam giác ABE, suy ra AD là đường trung tuyến của tam giác ABE.
+ Vì AD là đường phân giác đồng thời là đường trung tuyến trong tam giác ABE nên tam giác ABE cân tại A.
Lời giải chi tiết
Trong tam giác ABE có BC là đường trung tuyến, mà \(BD = 2DC\) nên D là trọng tâm của tam giác ABE. Vậy AD phải là đường trung tuyến của tam giác ABE.
Trong tam giác ABE có AD là đường phân giác đồng thời là đường trung tuyến nên tam giác ABE cân tại A.
Bài 4 (9.39) trang 88 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về biểu thức đại số và các phép toán trên biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán.
Đề bài yêu cầu chúng ta thực hiện các phép tính đại số, thường là rút gọn biểu thức hoặc tìm giá trị của biểu thức khi biết giá trị của biến. Việc hiểu rõ cấu trúc của biểu thức và áp dụng đúng các quy tắc là chìa khóa để giải quyết bài toán này.
(Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải cụ thể, giải thích rõ ràng từng bước và kết quả cuối cùng. Ví dụ:)
Ví dụ: Giả sử đề bài là: Rút gọn biểu thức 2x + 3y - x + 5y
Ngoài bài 4 (9.39) trang 88, Vở thực hành Toán 7 tập 2 còn có nhiều bài tập tương tự về biểu thức đại số. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp đã học ở trên. Một số dạng bài tập thường gặp bao gồm:
Kiến thức về biểu thức đại số có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học. Nó giúp chúng ta mô tả và giải quyết các vấn đề thực tế một cách hiệu quả. Ví dụ, trong vật lý, biểu thức đại số được sử dụng để mô tả các định luật và mối quan hệ giữa các đại lượng vật lý.
Bài 4 (9.39) trang 88 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về biểu thức đại số. Bằng cách nắm vững các khái niệm cơ bản, áp dụng đúng các quy tắc tính toán và thực hành thường xuyên, các em học sinh có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và phương pháp giải bài 4 (9.39) trang 88 Vở thực hành Toán 7 tập 2 đã giúp các em học sinh hiểu rõ hơn về bài tập này và tự tin hơn trong quá trình học tập.