Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 78 Vở thực hành Toán 7. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
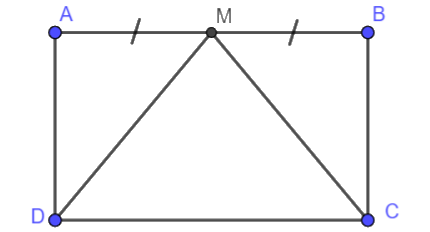
Bài 6. Cho hình chữ nhật ABCD và cho M là trung điểm của đoạn thẳng AB như hình vẽ dưới đây. Chứng minh rằng M nằm trên đường trung trực của CD.
Đề bài
Bài 6. Cho hình chữ nhật ABCD và cho M là trung điểm của đoạn thẳng AB như hình vẽ dưới đây. Chứng minh rằng M nằm trên đường trung trực của CD.
Phương pháp giải - Xem chi tiết
Chứng minh MD = MC.
Lời giải chi tiết
Hai tam giác MAD và MBC lần lượt vuông tại A, B và có:
MA = MB (M là trung điểm AB)
DA = CB (hai cạnh đối của hình chữ nhật)
Vậy \(\Delta MAD = \Delta MBC\)(hai cạnh góc vuông). Do đó MD = MC. Vậy M cách đều hai đầu của đoạn thẳng CD.
Do đó M nằm trên đường trung trực của đoạn thẳng CD.
Bài 6 trang 78 Vở thực hành Toán 7 thuộc chương trình học Toán lớp 7, thường liên quan đến các kiến thức về số nguyên, phép toán trên số nguyên, hoặc các bài toán ứng dụng thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán liên quan.
Thông thường, bài 6 trang 78 sẽ bao gồm một số câu hỏi hoặc bài tập nhỏ, yêu cầu học sinh:
Để giải bài 6 trang 78 Vở thực hành Toán 7, học sinh có thể áp dụng các phương pháp sau:
Bài tập: Tính giá trị của biểu thức: (-5) + 8 - (-3) + 2
Lời giải:
(-5) + 8 - (-3) + 2 = (-5) + 8 + 3 + 2 = 3 + 3 + 2 = 6 + 2 = 8
Ngoài các bài tập tính toán trực tiếp, bài 6 trang 78 Vở thực hành Toán 7 còn có thể xuất hiện các dạng bài tập sau:
Để đạt kết quả tốt nhất khi giải bài 6 trang 78 Vở thực hành Toán 7, học sinh cần lưu ý:
Học sinh có thể tham khảo thêm các tài liệu sau để hỗ trợ giải bài 6 trang 78 Vở thực hành Toán 7:
Bài 6 trang 78 Vở thực hành Toán 7 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số nguyên và các phép toán trên số nguyên. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.