Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 105, 106 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc ôn tập các kiến thức đã học về biểu thức đại số và các phép toán trên biểu thức.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho hai đa thức (A = 6{x^3} - 4{x^2} - 12x - 7) và (B = 2{x^2} - 7). a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho. b) Tính giá trị của đa thức (A + B) tại (x = - 2). c) Chứng minh rằng (x = 0,x = - 1) và (x = 2) là ba nghiệm của đa thức (A - B). d) Trình bày phép nhân A.B bằng hai cách. e) Tìm đa thức R có bậc nhỏ hơn 2 sao cho hiệu (A - R) chia hết cho B.
Đề bài
Cho hai đa thức \(A = 6{x^3} - 4{x^2} - 12x - 7\) và \(B = 2{x^2} - 7\).
a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho.
b) Tính giá trị của đa thức \(A + B\) tại \(x = - 2\).
c) Chứng minh rằng \(x = 0,x = - 1\) và \(x = 2\) là ba nghiệm của đa thức \(A - B\).
d) Trình bày phép nhân A.B bằng hai cách.
e) Tìm đa thức R có bậc nhỏ hơn 2 sao cho hiệu \(A - R\) chia hết cho B.
Phương pháp giải - Xem chi tiết
a) - Cho một đa thức. Khi đó:
+ Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất.
+ Hệ số của hạng tử bậc 0 (hạng tử không chứa biến) gọi là hệ số tự do.
b, c) + Để cộng (trừ) hai đa thức, ta viết hai đa thức trong dấu ngoặc và nối chúng bởi dấu “+” (hay “\( - \)”). Sau đó bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
+ Nếu tại \(x = a\) (a là một số), giá trị của một đa thức bằng 0 thì ta gọi a (hay \(x = a\)) là một nghiệm của đa thức đó.
+ Để tính giá trị đa thức tại \(x = - 2\), ta thay \(x = - 2\) vào đa thức \(A + B\) vừa tính ở trên, rút gọn ta thu được kết quả.
d) – Muốn một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
– Sử dụng cách đặt tính nhân để thực hiện phép tính:
+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.
+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau (để thực hiện phép cộng theo cột).
e) + Thực hiện phép chia A cho B được thương là Q và số dư là R, ta viết biểu thức dưới dạng \(A = B.Q + R\), từ đó tìm được đa thức R.
Lời giải chi tiết
a) Hệ số cao nhất của \(A = 6{x^3} - 4{x^2} - 12x - 7\) là 6 và hệ số tự do là -7.
Hệ số cao nhất của \(B = 2{x^2} - 7\) là 2 và hệ số tự do là -7.
b) Đặt \(S\left( x \right) = A + B\), ta có \(S\left( x \right) = \left( {6{x^3} - 4{x^2} - 12x - 7} \right) + \left( {2{x^2} - 7} \right) = 6{x^3} - 2{x^2} - 12x - 14\)
Giá trị của \(A + B\) tại \(x = - 2\) là: \(S\left( { - 2} \right) = 6.{\left( { - 2} \right)^3} - 2.{\left( { - 2} \right)^2} - 12.\left( { - 2} \right) - 14 = - 48 - 8 + 24 - 14 = - 46\)
c) Đặt \(D\left( x \right) = A - B\), ta có \(D\left( x \right) = \left( {6{x^3} - 4{x^2} - 12x - 7} \right) - \left( {2{x^2} - 7} \right) = 6{x^3} - 6{x^2} - 12x\)
Ta có: \(D\left( 0 \right) = 0;D\left( { - 1} \right) = 6.{\left( { - 1} \right)^3} - 6.{\left( { - 1} \right)^2} - 12.\left( { - 1} \right) = 0\) và \(D\left( 2 \right) = {6.2^3} - {6.2^2} - 12.2 = 0\).
Vậy \(x = 0,x = - 1\), \(x = 2\) là các nghiệm của D(x).
d) Cách 1: Khai triển tích:
\(A.B = \left( {6{x^3} - 4{x^2} - 12x - 7} \right)\left( {2{x^2} - 7} \right)\)
\( = 6{x^3}.2{x^2} - 4{x^2}.2{x^2} - 12x.2{x^2} - 7.2{x^2} - 7.6{x^3} + 7.4{x^2} + 7.12x + 7.7\)
\( = 12{x^5} - 8{x^4} - 24{x^3} - 14{x^2} - 42{x^3} + 28{x^2} + 84x + 49\)
\( = 12{x^5} - 8{x^4} - 66{x^3} + 14{x^2} + 84x + 49\)
Cách 2: Đặt tính nhân:
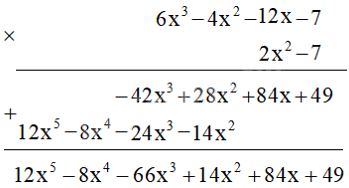
e) Chia A cho B bằng cách đặt tính chia:
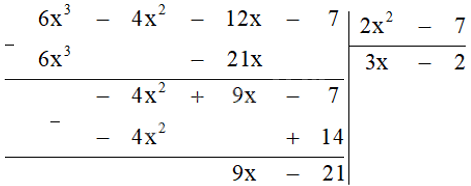
Từ đó suy ra: \(6{x^3} - 4{x^2} - 12x - 7 = \left( {2{x^2} - 7} \right)\left( {3x - 2} \right) + \left( {9x - 21} \right)\)
Nếu đặt \(R = 9x - 21\) thì đẳng thức trên có nghĩa là \(A = B.\left( {3x - 2} \right) + R\), suy ra \(A - R = B\left( {3x - 2} \right)\)
Vậy \(A - R\) chia hết cho B và đa thức cần tìm là \(R = 9x - 21\).
Bài 6 trong Vở thực hành Toán 7 tập 2 là một bài tập ôn tập quan trọng, giúp học sinh củng cố kiến thức về biểu thức đại số, các phép toán trên biểu thức, và cách áp dụng các quy tắc để đơn giản hóa biểu thức. Bài tập này thường bao gồm các dạng bài tập như:
Để giải bài 6 trang 105, 106 Vở thực hành Toán 7 tập 2 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Ví dụ 1: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Giải:
3x + 2y = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Ví dụ 2: Rút gọn biểu thức 2(x + 3) - 5x.
Giải:
2(x + 3) - 5x = 2x + 6 - 5x = -3x + 6
Để củng cố kiến thức và kỹ năng giải bài tập về biểu thức đại số, các em có thể tự giải các bài tập sau:
Khi giải bài tập về biểu thức đại số, các em cần chú ý:
Việc ôn tập biểu thức đại số là rất quan trọng đối với học sinh lớp 7, vì đây là nền tảng kiến thức để học các chương trình Toán học nâng cao hơn. Nắm vững kiến thức về biểu thức đại số sẽ giúp các em giải quyết các bài toán phức tạp một cách dễ dàng và hiệu quả hơn.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, và lời giải bài tập Toán 7, Toán 8, Toán 9. Chúng tôi luôn cố gắng tạo ra một môi trường học tập trực tuyến thân thiện, giúp các em học Toán một cách hiệu quả và thú vị.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 6 trang 105, 106 Vở thực hành Toán 7 tập 2 và đạt kết quả tốt trong môn Toán. Chúc các em học tập tốt!