Bài 3 (9.38) trang 87 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 (9.38) trang 87 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng: a) (AI < frac{1}{2}left( {AB + AC} right)); b) (AM < frac{1}{2}left( {AB + AC} right)).
Đề bài
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
a) \(AI < \frac{1}{2}\left( {AB + AC} \right)\);
b) \(AM < \frac{1}{2}\left( {AB + AC} \right)\).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(AI < AB\), \(AI < AC\) nên \(2AI < AB + AC\) hay \(AI < \frac{1}{2}\left( {AB + AC} \right)\).
b) + Lấy điểm D sao cho M là trung điểm của AD.
+ Chứng minh \(\Delta ABM = \Delta DCM\left( {c.g.c} \right)\), suy ra \(AB = CD\).
+ Chỉ ra \(AD < AC + DC\), suy ra \(2AM < AC + AB\), suy ra \(AM < \frac{1}{2}\left( {AB + AC} \right)\)
Lời giải chi tiết
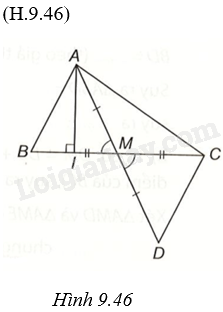
a) Trong tam giác vuông AIB có AB là cạnh huyền nên \(AI < AB\).
Trong tam giác vuông AIC có AC là cạnh huyền nên \(AI < AC\).
Suy ra \(2AI < AB + AC\) hay \(AI < \frac{1}{2}\left( {AB + AC} \right)\).
b) Lấy điểm D sao cho M là trung điểm của AD.
Xét \(\Delta ABM\) và \(\Delta DCM\) có: \(AM = MD,\widehat {AMB} = \widehat {DMC},MB = MC\), do đó, \(\Delta ABM = \Delta DCM\left( {c.g.c} \right)\).
Trong tam giác ACD, ta có \(AD < AC + DC\), suy ra \(2AM < AC + AB\), suy ra \(AM < \frac{1}{2}\left( {AB + AC} \right)\).
Bài 3 (9.38) trang 87 Vở thực hành Toán 7 tập 2 thuộc chương trình học về các phép toán với số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập 3 (9.38) trang 87 Vở thực hành Toán 7 tập 2 thường yêu cầu học sinh thực hiện các phép toán với số hữu tỉ, ví dụ như:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể:
(1/2) + (2/3) - (3/4)
Bước 1: Tìm mẫu số chung của các phân số.
Mẫu số chung của 2, 3 và 4 là 12.
Bước 2: Quy đồng các phân số về mẫu số chung.
(1/2) = (6/12)
(2/3) = (8/12)
(3/4) = (9/12)
Bước 3: Thực hiện phép cộng và trừ các phân số.
(6/12) + (8/12) - (9/12) = (6 + 8 - 9) / 12 = 5/12
Vậy, giá trị của biểu thức (1/2) + (2/3) - (3/4) là 5/12.
Để giải các bài tập về số hữu tỉ một cách nhanh chóng và chính xác, học sinh có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về số hữu tỉ, học sinh có thể tự giải các bài tập sau:
Bài 3 (9.38) trang 87 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về số hữu tỉ. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn đã cung cấp, các em học sinh sẽ tự tin hơn trong quá trình học tập.