Bài 5 (3.21) trang 46 Vở thực hành Toán 7 là một bài tập quan trọng trong chương trình học Toán lớp 7. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán số học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và chính xác nhất cho bài tập này, giúp học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
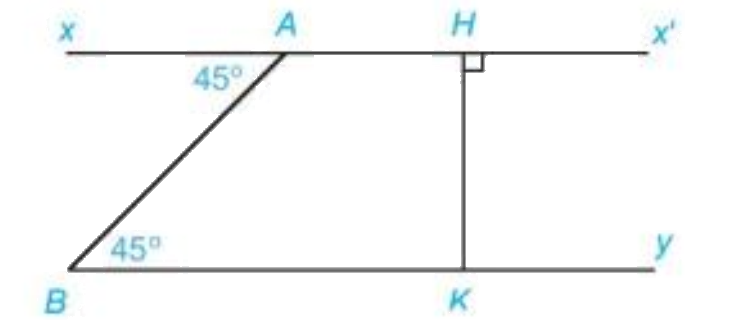
Bài 5 (3.21). Cho hình 3.15. Hãy giải thích tại sao: a) Ax’ // By; b) (By bot HK)
Đề bài
Bài 5 (3.21). Cho hình 3.15. Hãy giải thích tại sao:
a) Ax’ // By; b) \(By \bot HK\)
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong bằng nhau thì 2 đường thẳng đó song song
Lời giải chi tiết
a) Ta có \(\widehat {xAB} = \widehat {ABy} = {45^o}\) mà hai góc này ở vị trí so le trong
Suy ra Ax’ // By (dấu hiệu nhận biết hai đường thẳng song song)
b) Ta có \(HK \bot Ax'\) mà Ax’ // By suy ra \(By \bot HK\) .
Bài 5 (3.21) trang 46 Vở thực hành Toán 7 thuộc chương trình Toán lớp 7, tập trung vào việc rèn luyện kỹ năng thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ, cũng như các tính chất giao hoán, kết hợp, phân phối của các phép toán này.
Đề bài thường yêu cầu thực hiện các phép tính với số hữu tỉ, có thể là các phép cộng, trừ, nhân, chia đơn giản, hoặc các phép tính phức tạp hơn kết hợp nhiều phép toán. Ví dụ:
Để giải bài tập này, học sinh cần thực hiện theo các bước sau:
Ví dụ 1: Tính (1/2) + (1/3)
Giải:
(1/2) + (1/3) = (3/6) + (2/6) = (3+2)/6 = 5/6
Ví dụ 2: Tính (2/5) - (1/4)
Giải:
(2/5) - (1/4) = (8/20) - (5/20) = (8-5)/20 = 3/20
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, học sinh có thể luyện tập thêm các bài tập tương tự sau:
Bài 5 (3.21) trang 46 Vở thực hành Toán 7 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng thực hiện các phép toán với số hữu tỉ. Bằng cách nắm vững các quy tắc và tính chất của các phép toán này, cùng với việc luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.