Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trắc nghiệm trong Vở thực hành Toán 7. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những dạng bài tập mới.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán 7 một cách dễ dàng và hiệu quả nhất.
Hãy cùng khám phá lời giải chi tiết cho từng câu hỏi trắc nghiệm trang 13, 14 Vở thực hành Toán 7 ngay bây giờ!
Giá trị của \({\left( {{2^3}} \right)^5}\) :
Giá trị của \({\left( {{2^3}} \right)^5}\) :
A.\({2^8};\)
B.\({2^{15}};\)
C.\({\left( {\frac{1}{2}} \right)^{28}};\)
D.\(\frac{1}{2}\)
Phương pháp giải:
-Sử dụng công thức tính lũy thừa của lũy thừa.
Lời giải chi tiết:
Đáp án đúng là B
Ta có: \({\left( {{2^3}} \right)^5} = {2^{3.5}} = {2^{15}}.\)
Giá trị của \({\left( {\frac{1}{2}} \right)^7}:{\left( {\frac{1}{2}} \right)^4}\) là:
A.\({\left( {\frac{1}{2}} \right)^{11}};\)
B.\(\frac{1}{8};\)
C.\({\left( {\frac{1}{2}} \right)^{28}};\)
D.\(\frac{1}{2}.\)
Phương pháp giải:
- Ta sẽ sử dụng \({a^m} - {a^n} = {a^{m - n}}.\)
- Rồi sau đó ta sẽ tính lũy thừa
Lời giải chi tiết:
Đáp án đúng là B
\({\left( {\frac{1}{2}} \right)^7}:{\left( {\frac{1}{2}} \right)^4} = {\left( {\frac{1}{2}} \right)^{7 - 4}} = {\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}.\)
Giá trị của \(n\) bằng bao nhiêu nếu\({\left( {\frac{1}{3}} \right)^{n + 1}} = \frac{1}{{81}}.\)
A.2.
B.4.
C.1.
D.3.
Phương pháp giải:
-Ta sẽ quy đổi \(\frac{1}{{81}}\) bằng \(\frac{1}{3}\) mũ mấy đó
-Ta sẽ cho \(n + 1\) bằng số mũ vừa tìm, từ đó suy ra \(n\)
Lời giải chi tiết:
Đáp án đúng là D.
Ta có:\(\begin{array}{l}{\left( {\frac{1}{3}} \right)^{n + 1}} = \frac{1}{{81}}\\ \Leftrightarrow {\left( {\frac{1}{3}} \right)^{n + 1}} = {\left( {\frac{1}{3}} \right)^4}\\ \Leftrightarrow n + 1 = 4\\ \Leftrightarrow n = 3\end{array}\)
Vậy\(n = 3.\)
Giá trị của \({\left( {{2^3}} \right)^5}\) :
A.\({2^8};\)
B.\({2^{15}};\)
C.\({\left( {\frac{1}{2}} \right)^{28}};\)
D.\(\frac{1}{2}\)
Phương pháp giải:
-Sử dụng công thức tính lũy thừa của lũy thừa.
Lời giải chi tiết:
Đáp án đúng là B
Ta có: \({\left( {{2^3}} \right)^5} = {2^{3.5}} = {2^{15}}.\)
Giá trị của \({\left( {\frac{1}{2}} \right)^7}:{\left( {\frac{1}{2}} \right)^4}\) là:
A.\({\left( {\frac{1}{2}} \right)^{11}};\)
B.\(\frac{1}{8};\)
C.\({\left( {\frac{1}{2}} \right)^{28}};\)
D.\(\frac{1}{2}.\)
Phương pháp giải:
- Ta sẽ sử dụng \({a^m} - {a^n} = {a^{m - n}}.\)
- Rồi sau đó ta sẽ tính lũy thừa
Lời giải chi tiết:
Đáp án đúng là B
\({\left( {\frac{1}{2}} \right)^7}:{\left( {\frac{1}{2}} \right)^4} = {\left( {\frac{1}{2}} \right)^{7 - 4}} = {\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}.\)
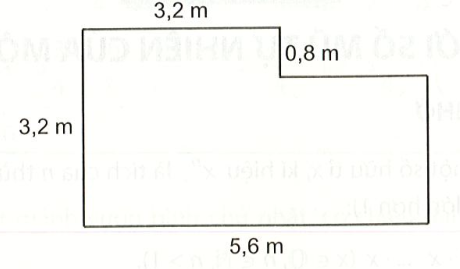
Diện tích của hình sau bằng
A.\(16{m^2};\)
B.\(17,92{m^2};\)
C.\(35,84{m^2};\)
D.\(24{m^2}.\)
Phương pháp giải:
-Ta sẽ chia hình thành 2 hình chữ nhật nhỏ rồi sau đó tính diện tích từng hình
-Rồi diện tích hình lớn bằng tổng diện tích 2 hình nhỏ.
Lời giải chi tiết:
Đáp án đúng là A.
Xét hình chữ nhật \(ABCD\) có chiều dài\(AB = 3,2m\) và chiều rộng \(BC = 0,8m.\)
Diện tích hình chữ nhật \(ABCD\) là: \(3,2.0,8 = 2,56{m^2}.\)
Xét hình chữ nhật \(DGFE\) có chiều dài \(EF = 5,6m\) và chiều rộng \(DE = AE - AD = 3,2 - 0,8 = 2,4m.\)
Diện tích hình chữ nhật \(DGFE\) là:
\(2,4.5,6 = 13,44{m^2}.\)
Diện tích của hình bằng tổng diện tích của hình chữ nhật \(ABCD\) và \(DGFE\) và bằng:
\(2,56 + 13,44 = 16{m^2}.\)
Giá trị của \(n\) bằng bao nhiêu nếu\({\left( {\frac{1}{3}} \right)^{n + 1}} = \frac{1}{{81}}.\)
A.2.
B.4.
C.1.
D.3.
Phương pháp giải:
-Ta sẽ quy đổi \(\frac{1}{{81}}\) bằng \(\frac{1}{3}\) mũ mấy đó
-Ta sẽ cho \(n + 1\) bằng số mũ vừa tìm, từ đó suy ra \(n\)
Lời giải chi tiết:
Đáp án đúng là D.
Ta có:\(\begin{array}{l}{\left( {\frac{1}{3}} \right)^{n + 1}} = \frac{1}{{81}}\\ \Leftrightarrow {\left( {\frac{1}{3}} \right)^{n + 1}} = {\left( {\frac{1}{3}} \right)^4}\\ \Leftrightarrow n + 1 = 4\\ \Leftrightarrow n = 3\end{array}\)
Vậy\(n = 3.\)
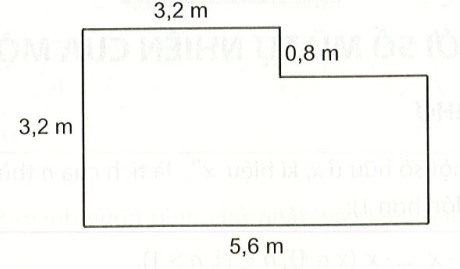
Diện tích của hình sau bằng
A.\(16{m^2};\)
B.\(17,92{m^2};\)
C.\(35,84{m^2};\)
D.\(24{m^2}.\)
Phương pháp giải:
-Ta sẽ chia hình thành 2 hình chữ nhật nhỏ rồi sau đó tính diện tích từng hình
-Rồi diện tích hình lớn bằng tổng diện tích 2 hình nhỏ.
Lời giải chi tiết:
Đáp án đúng là A.
Xét hình chữ nhật \(ABCD\) có chiều dài\(AB = 3,2m\) và chiều rộng \(BC = 0,8m.\)
Diện tích hình chữ nhật \(ABCD\) là: \(3,2.0,8 = 2,56{m^2}.\)
Xét hình chữ nhật \(DGFE\) có chiều dài \(EF = 5,6m\) và chiều rộng \(DE = AE - AD = 3,2 - 0,8 = 2,4m.\)
Diện tích hình chữ nhật \(DGFE\) là:
\(2,4.5,6 = 13,44{m^2}.\)
Diện tích của hình bằng tổng diện tích của hình chữ nhật \(ABCD\) và \(DGFE\) và bằng:
\(2,56 + 13,44 = 16{m^2}.\)
Trang 13 và 14 của Vở thực hành Toán 7 thường tập trung vào các chủ đề cơ bản như số nguyên, số hữu tỉ, các phép toán trên số nguyên và số hữu tỉ, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Các câu hỏi trắc nghiệm trang 13 thường kiểm tra khả năng hiểu và vận dụng các định nghĩa, tính chất của số nguyên và số hữu tỉ. Dưới đây là một số ví dụ và lời giải chi tiết:
Trang 14 thường đi sâu hơn vào các phép toán trên số hữu tỉ, bao gồm phép cộng, trừ, nhân, chia và các tính chất của chúng. Việc hiểu rõ các quy tắc và tính chất này sẽ giúp bạn giải quyết các bài tập một cách nhanh chóng và chính xác.
Trong quá trình giải các câu hỏi trắc nghiệm trang 13, 14 Vở thực hành Toán 7, bạn sẽ gặp một số dạng bài tập thường gặp sau:
Để giải quyết các dạng bài tập này một cách hiệu quả, bạn cần:
Khi giải bài tập trắc nghiệm, bạn cần chú ý một số điều sau:
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính chất giao hoán của phép cộng |
| (a + b) + c = a + (b + c) | Tính chất kết hợp của phép cộng |
| a * b = b * a | Tính chất giao hoán của phép nhân |
| (a * b) * c = a * (b * c) | Tính chất kết hợp của phép nhân |
Hy vọng với những lời giải chi tiết và phương pháp giải bài tập hiệu quả trên, bạn sẽ tự tin hơn khi giải các câu hỏi trắc nghiệm trang 13, 14 Vở thực hành Toán 7. Chúc bạn học tập tốt!