Bài 6 (2.11) trang 28 Vở thực hành Toán 7 là một bài tập quan trọng trong chương trình học Toán lớp 7. Bài tập này giúp học sinh rèn luyện kỹ năng thực hiện các phép tính với số hữu tỉ, đặc biệt là các phép cộng, trừ, nhân, chia.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 6 (2.11). Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo hình chữ nhật đó bằng bao nhiêu đề xi mét (làm tròn đến hàng phần mười)?
Đề bài
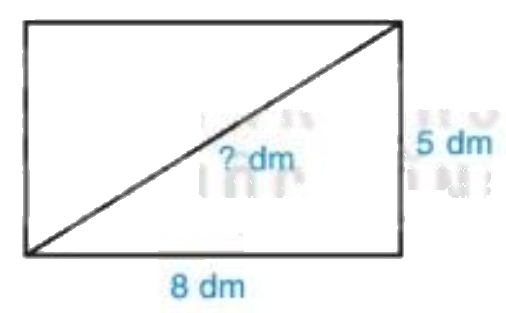
Bài 6 (2.11). Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo hình chữ nhật đó bằng bao nhiêu đề xi mét (làm tròn đến hàng phần mười)?
Phương pháp giải - Xem chi tiết
Tình tổng các bình phương độ dài hai cạnh của hình chữ nhật đó.
Lời giải chi tiết
Vì bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó ( theo gợi ý đề bài ) và hình chữ nhật đã cho có chiều dài 8dm, chiều rộng 5dm (giả thiết) nên độ dài đường chéo là \(\sqrt {{8^2} + {5^2}} = \sqrt {89} \). Sử dụng máy tính cầm tay ta tính được \(\sqrt {89} = 9,43398...\) Làm tròn đến hàng phần mười ta được 9,4. Độ dài đường chéo hình chữ nhật là 9,4 dm.
Bài 6 (2.11) trang 28 Vở thực hành Toán 7 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ.
Để giải bài 6 (2.11) trang 28 Vở thực hành Toán 7, chúng ta sẽ áp dụng các quy tắc đã nêu ở trên. Bài tập thường bao gồm các biểu thức số hữu tỉ cần tính toán. Dưới đây là ví dụ minh họa:
Ví dụ: Tính giá trị của biểu thức sau:
(1/2) + (2/3) - (1/4)
Giải:
Vậy, giá trị của biểu thức (1/2) + (2/3) - (1/4) là 11/12.
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, các em có thể luyện tập thêm với các bài tập tương tự trong Vở thực hành Toán 7 hoặc các tài liệu tham khảo khác.
Khi giải các bài tập về số hữu tỉ, các em nên chú ý:
Các phép tính với số hữu tỉ được ứng dụng rộng rãi trong đời sống hàng ngày, ví dụ như:
Bài 6 (2.11) trang 28 Vở thực hành Toán 7 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính toán với số hữu tỉ. Bằng cách nắm vững các quy tắc và áp dụng các phương pháp giải phù hợp, các em có thể tự tin giải quyết các bài tập tương tự và ứng dụng kiến thức vào thực tế.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 6 (2.11) trang 28 Vở thực hành Toán 7 và đạt kết quả tốt trong môn Toán.