Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 70, 71 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến biểu thức đại số và các phép toán cơ bản.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả. Hãy cùng chúng tôi khám phá lời giải chi tiết của bài 4 này nhé!
Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD. a) So sánh BK, BD. b) So sánh (BK + CN) với BC. c) Chứng minh (BK + CN < frac{1}{2}left( {AB + BC + CA} right)).
Đề bài
Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD.
a) So sánh BK, BD.
b) So sánh \(BK + CN\) với BC.
c) Chứng minh \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\).
Phương pháp giải - Xem chi tiết
a) Tam giác vuông BKD có BD là cạnh huyền nên \(BK < BD\).
b) + Từ a) suy ra \(BK + CN < BD + CN\).
+ Chứng minh tương tự: \(BD + CN < BD + CD\). Do đó, \(BK + CN < BD + CN < BD + CD = BC\).
c) + Chứng minh \(BK < AB\), \(CN < AC\).
+ Mà \(BK + CN < BC\) nên \(\left( {BK + CN} \right) + BK + CN < BC + AB + AC\), nên \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\)
Lời giải chi tiết
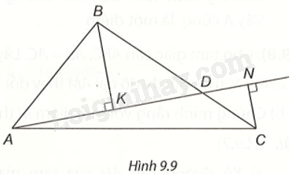
a) Trong tam giác vuông BKD có BD là cạnh huyền nên \(BK < BD\) (1)
b) Từ (1) suy ra \(BK + CN < BD + CN\) (2)
Trong tam giác vuông CND có DC là cạnh huyền nên \(NC < CD\), suy ra: \(BD + CN < BD + CD\). (3)
Từ (2) và (3) suy ra \(BK + CN < BD + CN < BD + CD = BC\).
Do đó, \(BK + CN < BC\). (4)
c) Trong tam giác vuông ABK có AB là cạnh huyền nên \(BK < AB\). (5)
Trong tam giác vuông CAN có AC là cạnh huyền nên \(CN < AC\). (6)
Từ (4), (5) và (6) suy ra \(\left( {BK + CN} \right) + BK + CN < BC + AB + AC\), hay \(2\left( {BK + CN} \right) < AB + BC + CA\), do đó \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\).
Bài 4 trang 70, 71 Vở thực hành Toán 7 tập 2 thường xoay quanh các dạng bài tập về thu gọn biểu thức đại số, tính giá trị của biểu thức, và thực hiện các phép toán với số hữu tỉ. Để giải quyết các bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng và phép trừ.
Để giúp các em hiểu rõ hơn về cách giải bài 4 trang 70, 71 Vở thực hành Toán 7 tập 2, chúng ta sẽ cùng nhau phân tích từng phần của bài tập.
Các bài tập trong phần này yêu cầu học sinh phải sử dụng các quy tắc về thứ tự thực hiện các phép toán và các tính chất của phép toán để thu gọn biểu thức đại số về dạng đơn giản nhất. Ví dụ:
Bài tập mẫu: Thu gọn biểu thức: 3x + 2y - x + 5y
Giải: 3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
Trong phần này, học sinh sẽ được cung cấp giá trị của các biến và yêu cầu tính giá trị của biểu thức. Để làm được điều này, học sinh cần thay thế các giá trị của biến vào biểu thức và thực hiện các phép toán theo đúng thứ tự.
Bài tập mẫu: Tính giá trị của biểu thức: 2x + 3y khi x = 1 và y = 2
Giải: 2x + 3y = 2 * 1 + 3 * 2 = 2 + 6 = 8
Các bài tập trong phần này yêu cầu học sinh phải thực hiện các phép cộng, trừ, nhân, chia với số hữu tỉ. Để giải quyết các bài tập này, học sinh cần nắm vững các quy tắc về phép toán với số hữu tỉ, bao gồm quy tắc cộng, trừ hai số hữu tỉ cùng mẫu, khác mẫu, quy tắc nhân, chia hai số hữu tỉ.
Bài tập mẫu: Tính: 1/2 + 1/3
Giải: 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Để nắm vững kiến thức và kỹ năng giải bài tập về biểu thức đại số và các phép toán cơ bản, học sinh nên dành thời gian luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng với đáp án chi tiết, giúp các em tự tin hơn trong quá trình học tập.
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin hơn trong việc giải bài 4 trang 70, 71 Vở thực hành Toán 7 tập 2. Chúc các em học tập tốt!