Bài 3 (9.12) trang 73 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.13). a) So sánh MB với (MN + NB), từ đó suy ra (MA + MB < NA + NB). b) So sánh NA với (CA + CN), từ đó suy ra (NA + NB < CA + CB). c) Chứng minh (MA + MB < CA + CB).
Đề bài
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.13).
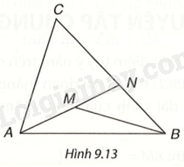
a) So sánh MB với \(MN + NB\), từ đó suy ra \(MA + MB < NA + NB\).
b) So sánh NA với \(CA + CN\), từ đó suy ra \(NA + NB < CA + CB\).
c) Chứng minh \(MA + MB < CA + CB\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra \(MB < MN + NB\), suy ra \(MA + MB < MA + MN + NB = NA + NB\).
b) Chỉ ra \(NA < CA + CN\), suy ra \(NA + NB < CA + NB + CN = CA + CB\).
c) Vì \(MA + MB < NA + NB\), \(NA + NB < CA + CB\) nên \(MA + MB < CA + CB\).
Lời giải chi tiết
a) Trong tam giác MNB ta có \(MB < MN + NB\), do đó
\(MA + MB < MA + MN + NB = NA + NB\) (vì \(MA + MN = NA\))
b) Trong tam giác ACN ta có \(NA < CA + CN\), do đó
\(NA + NB < CA + NB + CN = CA + CB\) (vì \(NB + NC = BC\))
c) Từ a) và b) ta có \(MA + MB < NA + NB\)
\(NA + NB < CA + CB\).
Suy ra \(MA + MB < NA + NB < CA + CB\).
Bài 3 (9.12) trang 73 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về biểu thức đại số và các phép toán số học để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phải phân tích đề bài, xác định đúng các yếu tố cần tìm và áp dụng các công thức, quy tắc đã học để đưa ra kết quả chính xác.
Thông thường, bài tập này sẽ bao gồm một hoặc nhiều câu hỏi yêu cầu học sinh thực hiện các phép tính, rút gọn biểu thức, hoặc giải phương trình đơn giản. Đề bài có thể được trình bày dưới dạng số hoặc chữ, đòi hỏi học sinh phải đọc kỹ và hiểu rõ yêu cầu trước khi bắt đầu giải.
Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Ngoài ra, học sinh cũng cần rèn luyện kỹ năng phân tích đề bài, xác định đúng các yếu tố cần tìm và áp dụng các công thức, quy tắc đã học một cách linh hoạt.
(Ở đây sẽ là lời giải chi tiết cho bài tập 3 (9.12) trang 73, bao gồm các bước giải cụ thể, giải thích rõ ràng và kết quả cuối cùng. Ví dụ:)
Ví dụ: Tính giá trị của biểu thức: 3x + 2y - 5z khi x = 2, y = -1, z = 3.
Giải:
Thay x = 2, y = -1, z = 3 vào biểu thức, ta được:
3x + 2y - 5z = 3(2) + 2(-1) - 5(3) = 6 - 2 - 15 = -11
Vậy, giá trị của biểu thức là -11.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo các bài tập tương tự sau:
Để đạt được kết quả tốt nhất khi giải bài tập này, học sinh cần:
Bài 3 (9.12) trang 73 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán và củng cố kiến thức đã học. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các phương pháp giải phù hợp và rèn luyện thường xuyên, học sinh có thể tự tin giải quyết bài tập này và đạt được kết quả tốt trong môn Toán.