Giải bài 3 (9.34) trang 84 Vở thực hành Toán 7 tập 2

Giải bài 3 (9.34) trang 84 vở thực hành Toán 7 tập 2

Giải bài 3 (9.34) trang 84 Vở thực hành Toán 7 tập 2

Bài 3 (9.34) trang 84 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 (9.34) trang 84 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 3 (9.34) trang 84 vở thực hành Toán 7 tập 2 1

+ Gọi tia đối của tia AC là tia Am.

+ Chỉ ra \(\widehat {{A_1}} = \widehat {{A_2}}\), \(\widehat {ABC} = \widehat {{A_2}},\widehat {ACB} = \widehat {{A_1}}\) nên \(\widehat {ABC} = \widehat {ACB}\).

Lời giải chi tiết

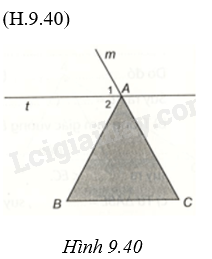
Giải bài 3 (9.34) trang 84 vở thực hành Toán 7 tập 2 2

Gọi tia đối của tia AC là Am. Ta có tia At chia góc mAB thành hai góc \(\widehat {{A_1}}\) và \(\widehat {{A_2}}\), \(\widehat {{A_1}} = \widehat {{A_2}}\).

Vì At//BC nên ta có \(\widehat {ABC} = \widehat {{A_2}},\widehat {ACB} = \widehat {{A_1}}\).

Suy ra \(\widehat {ACB} = \widehat {{A_1}} = \widehat {{A_2}} = \widehat {ABC}\). Vậy ABC là tam giác cân tại A.

Khai phá tiềm năng Toán lớp 7 của bạn! Đừng bỏ lỡ Giải bài 3 (9.34) trang 84 vở thực hành Toán 7 tập 2 tại chuyên mục giải toán 7 trên đề thi toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, cập nhật chính xác theo chương trình sách giáo khoa, các em sẽ tự tin ôn luyện, củng cố kiến thức vững chắc và nâng cao khả năng tư duy. Phương pháp học trực quan, sinh động sẽ mang lại hiệu quả học tập vượt trội mà bạn hằng mong muốn!

Giải bài 3 (9.34) trang 84 Vở thực hành Toán 7 tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 3 (9.34) trang 84 Vở thực hành Toán 7 tập 2 thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản sau:

Đa thức: Khái niệm về đa thức, các thành phần của đa thức (biến, hệ số, bậc).
Thu gọn đa thức: Cách thu gọn đa thức bằng cách cộng các đơn thức đồng dạng.
Bậc của đa thức: Cách xác định bậc của đa thức.
Giá trị của đa thức: Cách tính giá trị của đa thức tại một giá trị cụ thể của biến.

Lời giải chi tiết bài 3 (9.34) trang 84 Vở thực hành Toán 7 tập 2

Đề bài: (9.34) Tìm bậc của mỗi đa thức sau:

a) 5x⁴ + 2x² - 1
b) -2x³ + x² - 5x + 3
c) 7x⁵ - 3x + 4
d) 10x² - 4x

Giải:

a) Đa thức 5x⁴ + 2x² - 1 có bậc là 4.
b) Đa thức -2x³ + x² - 5x + 3 có bậc là 3.
c) Đa thức 7x⁵ - 3x + 4 có bậc là 5.
d) Đa thức 10x² - 4x có bậc là 2.

Phương pháp giải bài tập về bậc của đa thức

Để tìm bậc của một đa thức, ta cần xác định số mũ lớn nhất của biến trong đa thức đó. Các bước thực hiện như sau:

Xác định tất cả các đơn thức trong đa thức.
Xác định bậc của mỗi đơn thức. Bậc của một đơn thức là tổng số mũ của các biến trong đơn thức đó.
Chọn đơn thức có bậc lớn nhất. Bậc của đa thức là bậc của đơn thức đó.

Ví dụ minh họa

Tìm bậc của đa thức: 3x²y³ + 5xy - 2y² + 1

Giải:

Đơn thức 3x²y³ có bậc là 2 + 3 = 5.
Đơn thức 5xy có bậc là 1 + 1 = 2.
Đơn thức -2y² có bậc là 2.
Đơn thức 1 có bậc là 0.

Vậy, bậc của đa thức 3x²y³ + 5xy - 2y² + 1 là 5.

Bài tập luyện tập

Tìm bậc của các đa thức sau:

a) 4x³ - 2x² + x - 5
b) -x⁴ + 3x² - 7
c) 6x⁵y² - 4xy³ + 2x²y

Kết luận

Việc nắm vững kiến thức về đa thức và bậc của đa thức là rất quan trọng để giải các bài tập Toán 7. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự. Chúc các em học tốt!