Bài 6 (7.41) trang 51 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về tỉ lệ thức và giải bài toán liên quan đến tỉ lệ thức.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 (7.41) trang 51 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tìm số b sao cho đa thức ({x^3} - 3{x^2} + 2x - b) chia hết cho đa thức (x - 3).
Đề bài
Tìm số b sao cho đa thức \({x^3} - 3{x^2} + 2x - b\) chia hết cho đa thức \(x - 3\).
Phương pháp giải - Xem chi tiết
+ Thực hiện phép chia để tìm đa thức dư R(x) của phép chia.
+ Để phép chia là phép chia hết thì \(R\left( x \right) = 0\), từ đó tìm được b.
Lời giải chi tiết
Thực hiện phép chia để tìm đa thức dư:
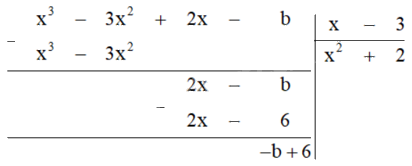
Vậy dư trong phép chia này là \( - b + 6\). Muốn có phép chia hết, dư trong phép chia này bằng 0, tức là \( - b + 6 = 0\). Từ đó suy ra \(b = 6\).
Bài 6 (7.41) trang 51 Vở thực hành Toán 7 tập 2 yêu cầu chúng ta giải một bài toán liên quan đến tỉ lệ thức. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về tỉ lệ thức, bao gồm định nghĩa, tính chất và các ứng dụng của tỉ lệ thức.
Cho tỉ lệ thức: a/b = c/d. Hãy chứng minh rằng:
(a + b) / (c + d) = a/c
(a - b) / (c - d) = a/c
Để giải các bài toán về tỉ lệ thức, chúng ta có thể sử dụng các phương pháp sau:
Sử dụng tính chất của tỉ lệ thức: Nếu a/b = c/d thì ad = bc và a/c = b/d, a+b/c+d = a/c, a-b/c-d = a/c.
Đặt ẩn phụ: Trong một số trường hợp, chúng ta có thể đặt ẩn phụ để đơn giản hóa bài toán.
Biến đổi đại số: Sử dụng các phép biến đổi đại số để đưa bài toán về dạng quen thuộc.
a) Chứng minh (a + b) / (c + d) = a/c
Vì a/b = c/d nên a = bc/d. Thay a = bc/d vào biểu thức (a + b) / (c + d), ta được:
(a + b) / (c + d) = (bc/d + b) / (c + d) = (bc + bd) / (d(c + d)) = b(c + d) / (d(c + d)) = b/d
Mà a/b = c/d nên a/c = b/d. Vậy (a + b) / (c + d) = a/c (đpcm)
b) Chứng minh (a - b) / (c - d) = a/c
Tương tự như trên, vì a/b = c/d nên a = bc/d. Thay a = bc/d vào biểu thức (a - b) / (c - d), ta được:
(a - b) / (c - d) = (bc/d - b) / (c - d) = (bc - bd) / (d(c - d)) = b(c - d) / (d(c - d)) = b/d
Mà a/b = c/d nên a/c = b/d. Vậy (a - b) / (c - d) = a/c (đpcm)
Để củng cố kiến thức về tỉ lệ thức, các em có thể tự giải các bài tập tương tự sau:
Bài 1: Cho tỉ lệ thức x/y = z/t. Chứng minh rằng (x + z) / (y + t) = x/y
Bài 2: Cho tỉ lệ thức a/b = c/d. Tính giá trị của biểu thức (2a - 3b) / (2c - 3d)
Hy vọng với lời giải chi tiết và phương pháp giải bài tập về tỉ lệ thức trên, các em học sinh sẽ hiểu rõ hơn về bài 6 (7.41) trang 51 Vở thực hành Toán 7 tập 2 và tự tin giải các bài tập tương tự. Chúc các em học tốt!