Bài 2 (4.2) trang 56 Vở thực hành Toán 7 là một bài tập quan trọng trong chương trình học Toán lớp 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 2 (4.2). Trong các tam giác dưới đây, tam giác nào nhọn, vuông, tù?
Đề bài
Bài 2 (4.2). Trong các tam giác dưới đây, tam giác nào nhọn, vuông, tù?
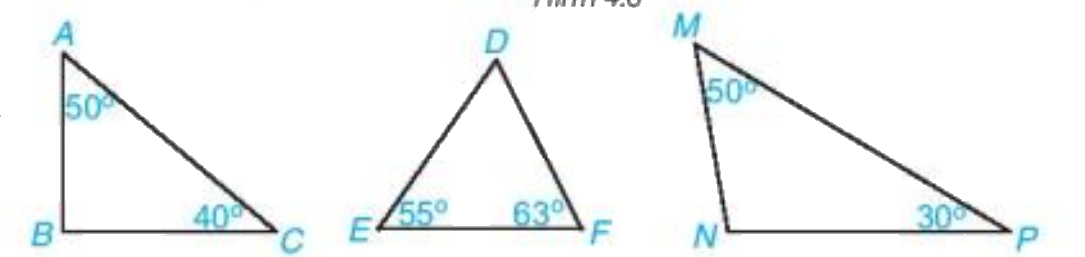
Phương pháp giải - Xem chi tiết
+ tam giác có ba góc đều nhọn là tam giác nhọn
+ tam giác có 1 góc tù là tam giác tù
+ tam giác có 1 góc vuông là tam giác vuông
Lời giải chi tiết
Vì tổng ba góc trong một tam giác bằng \({180^o}\) nên trong tam giác ABC ta có
\(\widehat A + \widehat B + \widehat C = {180^o} \Rightarrow \widehat B = {180^o} - \widehat A - \widehat C = {90^o}\)
Vậy tam giác ABC vuông tại B.
Tương tự trong tam giác DEF ta có
\(\widehat D + \widehat E + \widehat F = {180^o} \Rightarrow \widehat D = {180^o} - \widehat E - \widehat F = {62^o}\)
Vậy cả 3 góc của tam giác DEF đều là góc nhọn nên tam giác DEF là tam giác nhọn.
Cuối cùng tỏng tam giác MNP ta có
\(\widehat M + \widehat N + \widehat P = {180^o} \Rightarrow \widehat N = {180^o} - \widehat M - \widehat P = {100^o}\)
Vậy tam giác MNP có góc N là góc tù nên MNP là tam giác tù.
Kết luận: Tam giác ABC vuông, tam giác DEF nhọn và tam giác MNP tù.
Bài 2 (4.2) trang 56 Vở thực hành Toán 7 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về phép cộng, trừ, nhân, chia số hữu tỉ, cũng như các tính chất của phép toán.
Bài tập 2 (4.2) thường bao gồm các câu hỏi yêu cầu học sinh thực hiện các phép tính sau:
Để giải bài tập này, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Tính (-1/2) + (3/4)
Giải:
Vậy, (-1/2) + (3/4) = 1/4
Số hữu tỉ là tập hợp các số có thể biểu diễn dưới dạng phân số a/b, trong đó a là số nguyên và b là số nguyên khác 0. Số hữu tỉ bao gồm số nguyên, số phân số và số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Các phép toán trên số hữu tỉ tuân theo các quy tắc tương tự như các phép toán trên số nguyên, tuy nhiên cần lưu ý đến quy tắc dấu và quy đồng mẫu số khi cộng, trừ.
Để củng cố kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ, học sinh có thể thực hiện thêm các bài tập sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập 2 (4.2) trang 56 Vở thực hành Toán 7 và đạt kết quả tốt trong môn Toán.
| Phép toán | Quy tắc |
|---|---|
| Cộng hai số hữu tỉ cùng dấu | Cộng các giá trị tuyệt đối và giữ nguyên dấu |
| Cộng hai số hữu tỉ khác dấu | Lấy giá trị tuyệt đối của số lớn trừ giá trị tuyệt đối của số nhỏ và giữ nguyên dấu của số lớn |
| Nhân hai số hữu tỉ cùng dấu | Nhân các giá trị tuyệt đối và kết quả dương |
| Nhân hai số hữu tỉ khác dấu | Nhân các giá trị tuyệt đối và kết quả âm |