Bài 8 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Bài tập này thường yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ, đồng thời áp dụng các quy tắc về dấu và thứ tự thực hiện các phép toán.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 107,108 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho (DM = DC). a) Chứng minh rằng (Delta ADM = Delta BDC). Từ đó suy ra (AM = BC) và AM//BC. b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho (EN = EB). Chứng minh rằng AN//BC. c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.
Đề bài
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho \(DM = DC\).
a) Chứng minh rằng \(\Delta ADM = \Delta BDC\). Từ đó suy ra \(AM = BC\) và AM//BC.
b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho \(EN = EB\). Chứng minh rằng AN//BC.
c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.
Phương pháp giải - Xem chi tiết
a) Chỉ ra \(AD = DB\), \(\widehat {ADM} = \widehat {BDC}\), \(DM = DC\) suy ra \(\Delta ADM = \Delta BDC\) (c.g.c), suy ra \(AM = BC\) và \(\widehat {MAD} = \widehat {CBD}\), suy ra AM//BC.
b) Chứng minh \(\Delta AEN = \Delta CEB\) (c.g.c), suy ra \(\widehat {EAN} = \widehat {ECB}\), suy ra AN//BC.
c) + Ta có AM//BC, AN//BC nên AM và AN trùng nhau, suy ra ba điểm M, A, N thẳng hàng.
+ Vì \(AM = BC\) và \(AN = BC\), suy ra \(AM = AN\) nên A là trung điểm của MN.
Lời giải chi tiết
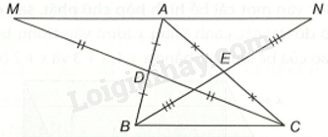
a) \(\Delta ADM\) và \(\Delta BDC\) có:
\(AD = DB\) (do D là trung điểm của AB).
\(\widehat {ADM} = \widehat {BDC}\) (hai góc đối đỉnh)
\(DM = DC\) (giả thiết)
Nên \(\Delta ADM = \Delta BDC\) (c.g.c).
Suy ra \(AM = BC\) (hai cạnh tương ứng) và \(\widehat {MAD} = \widehat {CBD}\) (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AM//BC (dấu hiệu nhận biết hai đường thẳng song song).
b) \(\Delta AEN\) và \(\Delta CEB\) có:
\(AE = CE\) (do E là trung điểm của AC).
\(\widehat {AEN} = \widehat {CEB}\) (hai góc đối đỉnh)
\(EN = EB\) (theo giả thiết)
Nên \(\Delta AEN = \Delta CEB\) (c.g.c).
Suy ra \(\widehat {EAN} = \widehat {ECB}\) (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AN//BC (dấu hiệu nhận biết hai đường thẳng song song).
c) Ta có AM//BC (chứng minh trên), AN//BC (chứng minh trên) nên AM và AN trùng nhau (theo tiên đề Euclid).
Từ đó suy ra ba điểm M, A, N thẳng hàng.
Ta lại có \(AM = BC\) (chứng minh trên) và \(AN = BC\) (chứng minh trên), do đó \(AM = AN\).
Từ đó suy ra A là trung điểm của MN.
Bài 8 trong Vở thực hành Toán 7 tập 2 tập trung vào việc vận dụng các kiến thức đã học về số hữu tỉ để thực hiện các phép tính. Nội dung bài tập thường bao gồm các biểu thức số học, yêu cầu học sinh tính toán chính xác và hợp lý. Việc nắm vững các quy tắc về dấu, thứ tự thực hiện các phép toán, và các tính chất của phép cộng, trừ, nhân, chia số hữu tỉ là vô cùng quan trọng để giải quyết bài tập này một cách hiệu quả.
Bài 8 thường bao gồm nhiều câu nhỏ, mỗi câu yêu cầu học sinh thực hiện một phép tính cụ thể. Các phép tính này có thể là:
Ngoài ra, bài tập còn có thể yêu cầu học sinh thực hiện các phép tính kết hợp nhiều phép toán khác nhau trong một biểu thức. Ví dụ: (1/2 + 3/4) * (-2/5)
Để giải bài 8 trang 107,108 Vở thực hành Toán 7 tập 2 một cách hiệu quả, học sinh cần:
Ví dụ 1: Tính -2/3 + 1/2
Giải:
-2/3 + 1/2 = -4/6 + 3/6 = -1/6
Ví dụ 2: Tính 3/4 * (-2/5)
Giải:
3/4 * (-2/5) = -6/20 = -3/10
Khi giải bài 8 trang 107,108 Vở thực hành Toán 7 tập 2, học sinh cần chú ý:
Để củng cố kiến thức và kỹ năng giải bài 8, học sinh có thể tự giải các bài tập tương tự sau:
Bài 8 trang 107,108 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Việc nắm vững các quy tắc và thực hành thường xuyên sẽ giúp học sinh tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.