Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 75 Vở thực hành Toán 7 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em tự tin hơn trong việc chinh phục môn Toán.
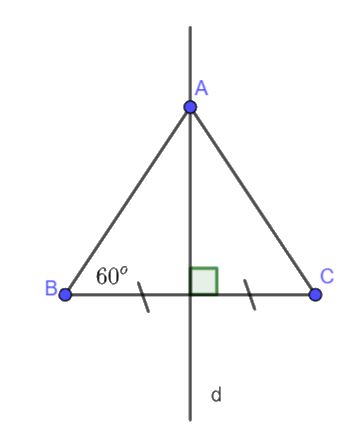
Bài 8. Cho điểm A nằm trên trung trực của đoạn thẳng BC sao cho \(\widehat {ABC} = {60^o}\). Chứng minh rằng CA = CB.
Đề bài
Bài 8. Cho điểm A nằm trên trung trực của đoạn thẳng BC sao cho \(\widehat {ABC} = {60^o}\). Chứng minh rằng CA = CB.
Phương pháp giải - Xem chi tiết
Chứng minh ABC là tam giác đều
Lời giải chi tiết
GT | d là trung trực BC, \(A \in BC,\widehat {ABC} = {60^o}\) |
KL | CA = CB. |
Do A thuộc trung trực BC nên AB = AC hay \(\Delta ABC\)cân tại A.
Từ đây suy ra \(\widehat {ACB} = \widehat {ABC} = {60^o}\). Do tổng ba góc trong tam giác ABC bằng \({180^o}\)nên:
\(\widehat {BAC} = {180^o} - \widehat {ACB} - \widehat {ABC} = {60^o}\)
Vậy tam giác ABC có ba góc bằng nhau nên ABC là tam giác đều và do đó CA = CB.
Bài 8 trang 75 Vở thực hành Toán 7 thuộc chương trình học Toán lớp 7, tập trung vào việc vận dụng các kiến thức về biểu thức đại số, các phép toán với số hữu tỉ, và các tính chất của phép cộng, trừ, nhân, chia. Mục tiêu chính của bài tập này là giúp học sinh rèn luyện kỹ năng biến đổi biểu thức, tính toán chính xác, và áp dụng kiến thức vào giải quyết các bài toán thực tế.
Bài 8 thường bao gồm các dạng bài tập sau:
Để tính giá trị của biểu thức đại số, ta thay giá trị của các biến đã cho vào biểu thức và thực hiện các phép toán theo đúng thứ tự ưu tiên (ngoặc, lũy thừa, nhân chia, cộng trừ). Ví dụ:
Cho biểu thức A = 2x + 3y với x = 1 và y = -2. Tính giá trị của A.
Giải:
A = 2 * 1 + 3 * (-2) = 2 - 6 = -4
Để rút gọn biểu thức đại số, ta sử dụng các tính chất của phép toán như tính chất giao hoán, tính chất kết hợp, tính chất phân phối để biến đổi biểu thức về dạng đơn giản nhất. Ví dụ:
Rút gọn biểu thức B = 3x + 5y - 2x + y
Giải:
B = (3x - 2x) + (5y + y) = x + 6y
Để tìm x, ta thực hiện các phép toán để đưa x về một vế của phương trình và các số còn lại về vế kia. Sau đó, ta chia cả hai vế của phương trình cho hệ số của x để tìm ra giá trị của x. Ví dụ:
Tìm x biết 2x + 5 = 11
Giải:
2x = 11 - 5 = 6
x = 6 / 2 = 3
Các bài tập ứng dụng thực tế thường yêu cầu học sinh vận dụng kiến thức về biểu thức đại số để giải quyết các vấn đề liên quan đến cuộc sống hàng ngày. Ví dụ:
Một người mua 3 kg táo với giá x đồng một kg và 2 kg cam với giá y đồng một kg. Tính tổng số tiền người đó phải trả.
Giải:
Tổng số tiền người đó phải trả là 3x + 2y đồng.
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong Vở thực hành Toán 7 và các tài liệu tham khảo khác.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải bài 8 trang 75 Vở thực hành Toán 7. Chúc các em học tập tốt!