Bài 3 (7.14) trang 34 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hai đa thức (A = 6{x^4} - 4{x^3} + x - frac{1}{3}) và (B = - 3{x^4} - 2{x^3} - 5{x^2} + x + frac{2}{3}). Tính (A + B) và (A - B).
Đề bài
Cho hai đa thức \(A = 6{x^4} - 4{x^3} + x - \frac{1}{3}\) và \(B = - 3{x^4} - 2{x^3} - 5{x^2} + x + \frac{2}{3}\). Tính \(A + B\) và \(A - B\).
Phương pháp giải - Xem chi tiết
Để cộng (trừ) hai đa thức:
Cách 1: Viết hai đa thức trong dấu ngoặc và nối chúng bởi dấu “+” (hay “\( - \)”). Sau đó bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc của hai đa thức thì thẳng cột với nhau rồi cộng (trừ) theo từng cột.
Lời giải chi tiết
Cách thứ nhất:
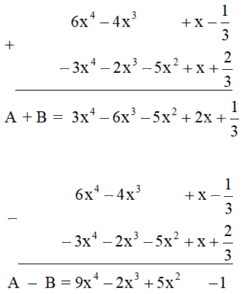
Cách thứ hai:
\(A + B = \left( {6{x^4} - 4{x^3} + x - \frac{1}{3}} \right) + \left( { - 3{x^4} - 2{x^3} - 5{x^2} + x + \frac{2}{3}} \right)\)
\( = \left( {6{x^4} - 3{x^4}} \right) + \left( { - 4{x^3} - 2{x^3}} \right) - 5{x^2} + \left( {x + x} \right) + \left( { - \frac{1}{3} + \frac{2}{3}} \right)\)
\( = 3{x^4} - 6{x^3} - 5{x^2} + 2x + \frac{1}{3}\)
\(A - B = \left( {6{x^4} - 4{x^3} + x - \frac{1}{3}} \right) - \left( { - 3{x^4} - 2{x^3} - 5{x^2} + x + \frac{2}{3}} \right)\)
\( = 6{x^4} - 4{x^3} + x - \frac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} - x - \frac{2}{3}\)
\( = \left( {6{x^4} + 3{x^4}} \right) + \left( { - 4{x^3} + 2{x^3}} \right) + 5{x^2} + \left( {x - x} \right) + \left( { - \frac{1}{3} - \frac{2}{3}} \right)\)
\( = 9{x^4} - 2{x^3} + 5{x^2} - 1\)
Bài 3 (7.14) trang 34 Vở thực hành Toán 7 tập 2 thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức về tỉ lệ thức và tính chất của dãy tỉ số bằng nhau để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ kiểm tra và thi học kỳ, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Để bắt đầu, chúng ta cùng xem lại đề bài chính xác:
(Đề bài sẽ được chèn vào đây - ví dụ: Cho tỉ lệ thức a/b = c/d. Chứng minh rằng (a+b)/(a-b) = (c+d)/(c-d))
Để giải quyết bài tập này, chúng ta cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho bài tập này:
(Lời giải chi tiết sẽ được chèn vào đây, bao gồm các bước giải, giải thích rõ ràng và sử dụng các ký hiệu toán học chính xác. Ví dụ:
Từ a/b = c/d, ta có ad = bc.
Cộng b vào cả hai vế: ad + b2 = bc + b2
Phân tích thành nhân tử: d(a+b) = b(c+b)
Suy ra (a+b)/b = (c+b)/d (1)
Tương tự, trừ b vào cả hai vế của ad = bc: ad - b2 = bc - b2
Phân tích thành nhân tử: d(a-b) = b(c-b)
Suy ra (a-b)/b = (c-b)/d (2)
Từ (1) và (2), ta có thể suy ra (a+b)/(a-b) = (c+d)/(c-d) (đpcm)
)Để củng cố kiến thức và kỹ năng giải bài tập về tỉ lệ thức, bạn có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về tỉ lệ thức, bạn cần lưu ý những điều sau:
Bài 3 (7.14) trang 34 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về tỉ lệ thức. Hy vọng với hướng dẫn chi tiết và lời giải trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.