Chào mừng các em học sinh đến với lời giải chi tiết bài 4 (9.35) trang 84, 85 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Kí hiệu ({S_{ABC}}) là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC. a) Chứng minh ({S_{GBC}} = frac{1}{3}{S_{ABC}}). Gợi ý. Sử dụng (GM = frac{1}{3}AM) để chứng minh ({S_{GBM}} = frac{1}{3}{S_{ABM}},{S_{GCM}} = frac{1}{3}{S_{ACM}}). b) Chứng minh ({S_{GCA}} = {S_{GAB}} = frac{1}{3}{S_{ABC}}). Nhận xét. Từ bài tập trên ta có: ({S_{GBC}} = {S_{GCA}} = {S_{GAB}} = frac{1}{3}{S_{ABC}}), điều này giúp ta cảm nhận tại sao có thể đặt thăng b
Đề bài
Kí hiệu \({S_{ABC}}\) là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC.
a) Chứng minh \({S_{GBC}} = \frac{1}{3}{S_{ABC}}\).
Gợi ý. Sử dụng \(GM = \frac{1}{3}AM\) để chứng minh \({S_{GBM}} = \frac{1}{3}{S_{ABM}},{S_{GCM}} = \frac{1}{3}{S_{ACM}}\).
b) Chứng minh \({S_{GCA}} = {S_{GAB}} = \frac{1}{3}{S_{ABC}}\).
Nhận xét. Từ bài tập trên ta có: \({S_{GBC}} = {S_{GCA}} = {S_{GAB}} = \frac{1}{3}{S_{ABC}}\), điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó.
Phương pháp giải - Xem chi tiết
a) Vì \(GM \) \(= \frac{1}{3}AM\), suy ra \({S_{GBM}} \) \(= \frac{1}{3}{S_{ABM}},{S_{GCM}} \) \(= \frac{1}{3}{S_{ACM}}\).
Suy ra: \({S_{GBC}} \) \(= {S_{BGM}} + {S_{CGM}} \) \(= \frac{1}{3}{S_{ABM}} + \frac{1}{3}{S_{ACM}} \) \(= \frac{1}{3}\left( {{S_{ABM}} + {S_{ACM}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\)
b) + Tương tự phần a ta có: \({S_{GAC}} \) \(= {S_{CGN}} + {S_{AGN}} \) \(= \frac{1}{3}{S_{BCN}} + \frac{1}{3}{S_{ABN}} \) \(= \frac{1}{3}{S_{ABC}}\), \({S_{GAB}} \) \(= {S_{BGP}} + {S_{AGP}} \) \(= \frac{1}{3}{S_{BCP}} + \frac{1}{3}{S_{APC}} \) \(= \frac{1}{3}{S_{ABC}}\).
Lời giải chi tiết
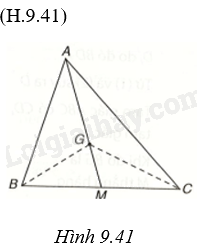
a) Ta có \({S_{GBC}} \) \(= {S_{BGM}} + {S_{CGM}}\).
Vì G là trọng tâm của tam giác ABC nên \(GM \) \(= \frac{1}{3}AM\), suy ra \({S_{GBM}} \) \(= \frac{1}{3}{S_{ABM}},{S_{GCM}} \) \(= \frac{1}{3}{S_{ACM}}\).
Suy ra: \({S_{GBC}} \) \(= {S_{BGM}} + {S_{CGM}} \) \(= \frac{1}{3}{S_{ABM}} + \frac{1}{3}{S_{ACM}} \) \(= \frac{1}{3}\left( {{S_{ABM}} + {S_{ACM}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\).
b) Tương tự \(GN \) \(= \frac{1}{3}BN\) nên
\({S_{GAC}} \) \(= {S_{CGN}} + {S_{AGN}} \) \(= \frac{1}{3}{S_{BCN}} + \frac{1}{3}{S_{ABN}} \) \(= \frac{1}{3}\left( {{S_{BCN}} + {S_{ABN}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\)
Vì \(GP \) \(= \frac{1}{3}CP\) nên
\({S_{GAB}} \) \(= {S_{BGP}} + {S_{AGP}} \) \(= \frac{1}{3}{S_{BCP}} + \frac{1}{3}{S_{APC}} \) \(= \frac{1}{3}\left( {{S_{BCP}} + {S_{APC}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\)
Vậy \({S_{GBC}} \) \(= {S_{GCA}} \) \(= {S_{GAB}} \) \(= \frac{1}{3}{S_{ABC}}\)
Bài 4 (9.35) trang 84, 85 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán liên quan đến các biểu thức đại số và các phép toán cơ bản. Bài tập này yêu cầu học sinh phải nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất của phép cộng, phép trừ, phép nhân, phép chia và các quy tắc về dấu ngoặc.
Bài 4 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các phép tính đại số khác nhau. Để giải bài tập này một cách hiệu quả, học sinh cần:
Để giải phần a, ta cần thực hiện các phép tính trong ngoặc trước, sau đó thực hiện các phép tính nhân, chia, cộng, trừ theo thứ tự từ trái sang phải. Ví dụ:
(2x + 3y) * 4 = 8x + 12y
Tương tự như phần a, ta cần thực hiện các phép tính trong ngoặc trước, sau đó thực hiện các phép tính nhân, chia, cộng, trừ theo thứ tự từ trái sang phải. Ví dụ:
(5a - 2b) / 2 = 2.5a - b
Phần c có thể yêu cầu học sinh rút gọn biểu thức hoặc tìm giá trị của biểu thức khi biết giá trị của các biến. Ví dụ:
Nếu a = 2 và b = 3, thì 5a - 2b = 5 * 2 - 2 * 3 = 10 - 6 = 4
Ngoài bài 4, Vở thực hành Toán 7 tập 2 còn có nhiều bài tập tương tự, yêu cầu học sinh rèn luyện các kỹ năng giải toán đại số khác nhau. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập đại số một cách hiệu quả, học sinh có thể áp dụng một số mẹo sau:
Để học tập và rèn luyện thêm kiến thức về Toán 7, học sinh có thể tham khảo các tài liệu sau:
Bài 4 (9.35) trang 84, 85 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng giải toán đại số. Bằng cách nắm vững các quy tắc, tính chất và áp dụng các mẹo giải bài tập hiệu quả, học sinh có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.