Bài 7 trang 51, 52 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ, đặc biệt là các phép cộng, trừ, nhân, chia số hữu tỉ.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7 trang 51, 52 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Sau khi thực hiện phép nhân hai đa thức bằng cách đặt tính nhân, Toàn tinh nghịch xóa đi một số hạng tử (đơn thức) và đánh dấu các hạng tử bị xóa bởi các chữ cái a, b, c… như sau (bao gồm cả dấu của hạng tử đó): Toàn đố Thắng tìm lại các hạng tử bị xóa để khôi phục lại phép tính ban đầu. Biết rằng quá trình tính toán Toàn đều làm đúng và hai chữ cái khác nhau có thể thay thế cho hai hạng tử giống nhau hay khác nhau. Em hãy giúp Thắng giải bài đố này nhé.
Đề bài
Sau khi thực hiện phép nhân hai đa thức bằng cách đặt tính nhân, Toàn tinh nghịch xóa đi một số hạng tử (đơn thức) và đánh dấu các hạng tử bị xóa bởi các chữ cái a, b, c… như sau (bao gồm cả dấu của hạng tử đó):

Toàn đố Thắng tìm lại các hạng tử bị xóa để khôi phục lại phép tính ban đầu. Biết rằng quá trình tính toán Toàn đều làm đúng và hai chữ cái khác nhau có thể thay thế cho hai hạng tử giống nhau hay khác nhau. Em hãy giúp Thắng giải bài đố này nhé.
Phương pháp giải - Xem chi tiết
+ Vì \(2.\left( { - 5} \right) = e = p = - 10\) và \(g = 5{x^3}\).
+ Vì \(2x = 2.b\) nên tìm được b.
+ Từ \({x^2} = c.b = c.x\) nên tìm được c.
+ Từ \(h = c.\left( { - 5} \right) = - 5x\) nên tính được h.
+ Từ \(g = 5{x^3}\) và \(g = c.a\) nên tìm được a.
+ Vì \(d = 2.a\) nên tính được a.
+ Vì \(n = 2x + h\) và \(m = d + {x^2}\) nên tính được m và n.
Lời giải chi tiết
(Để cho dễ phân biệt, trong kết quả, ta sẽ viết các đơn thức kèm theo dấu của nó).
- Dễ thấy ta phải có \(2.\left( { - 5} \right) = e = p = - 10\) và \(g = 5{x^3}\).
- Trong dòng thứ ba, ta có \(2x = 2.b\). Từ đó suy ra \(b = x\).
- Trong dòng thứ tư, ta có \({x^2} = c.b = c.x\), suy ra \(c = x\).
- Tiếp theo, trong dòng thứ tư, ta có \(h = c.\left( { - 5} \right) = - 5x\). Vậy \(h = - 5x\).
- Trên đây ta đã có \(g = 5{x^3}\). Mặt khác, \(g = c.a\) nên \(5{x^3} = x.a\). Vậy \(a = 5{x^2}\). Từ kết quả này ta còn suy ra \(d = 2.a = 2.5{x^2} = 10{x^2}\), tức là \(d = 10{x^2}\).
- Cuối cùng, ta được \(n = 2x + h = 2x - 5x = - 3x\) và \(m = d + {x^2} = 10{x^2} + {x^2} = 11{x^2}\).
Kết quả, phép nhân mà Toàn đã thực hiện là:
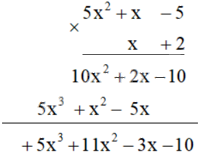
Bài 7 trong Vở thực hành Toán 7 tập 2 tập trung vào việc vận dụng các quy tắc cộng, trừ, nhân, chia số hữu tỉ để tính toán các biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 7 trang 51, 52 Vở thực hành Toán 7 tập 2:
Tính: (-1/2) + (3/4)
Lời giải:
Vậy, (-1/2) + (3/4) = 1/4
Tính: (2/3) - (-1/6)
Lời giải:
Vậy, (2/3) - (-1/6) = 5/6
Tính: (1/2) * (-3/4)
Lời giải:
Vậy, (1/2) * (-3/4) = -3/8
Tính: (-5/6) : (2/3)
Lời giải:
Vậy, (-5/6) : (2/3) = -5/4
Để củng cố kiến thức về các phép toán với số hữu tỉ, các em có thể tự giải thêm các bài tập sau:
Khi giải các bài tập về số hữu tỉ, các em nên:
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em học sinh sẽ tự tin hơn khi giải bài 7 trang 51, 52 Vở thực hành Toán 7 tập 2 và đạt kết quả tốt trong môn Toán.