Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 102 sách bài tập toán 9 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
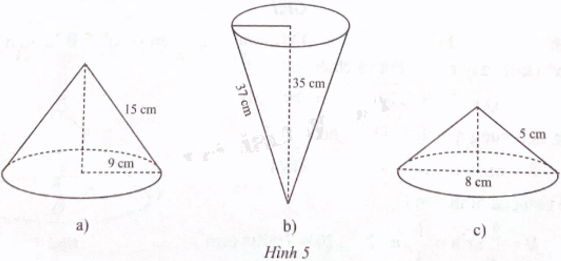
Hãy cho biết bán kính đáy, chiều cao, độ dài đường sinh của mỗi hình nó sau:
Đề bài
Hãy cho biết bán kính đáy, chiều cao, độ dài đường sinh của mỗi hình nó sau:
Phương pháp giải - Xem chi tiết
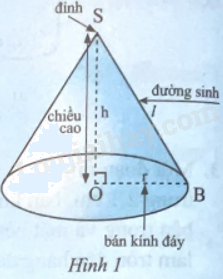
Khi quay tam giác vuông SOB một vòng quanh cạnh góc vuông SO cố định ta được một hình nón (Hình 1).
Lời giải chi tiết
a) Chiều cao hình nón: h = \(\sqrt {{{15}^2} - {9^2}} = 12\) (cm).
Bán kính đáy, chiều cao, độ dài đường sinh của hình nón lần lượt là 9 cm, 12 cm, 15 cm.
b) Bán kính đáy của hình nón là: r = \(\sqrt {{{37}^2} - {{35}^2}} = 12\)(cm).
Bán kính đáy, chiều cao, độ dài đường sinh của hình nón lần lượt là 12 cm, 35 cm, 37 cm.
c) Chiều cao hình nón: h = \(\sqrt {{5^2} - {4^2}} = 3\) (cm).
Bán kính đáy, chiều cao, độ dài đường sinh của hình nón lần lượt là 4 cm, 3 cm, 5 cm.
Bài 1 trang 102 sách bài tập toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 trang 102 sách bài tập toán 9 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giúp bạn giải bài 1 trang 102 sách bài tập toán 9 - Chân trời sáng tạo tập 2 một cách dễ dàng, chúng tôi sẽ cung cấp lời giải chi tiết cho từng phần của bài tập. Dưới đây là hướng dẫn giải:
Để xác định hàm số bậc nhất, bạn cần tìm các hệ số a và b. Hãy sử dụng các thông tin cho trước trong đề bài để lập phương trình và giải tìm a và b. Ví dụ, nếu đề bài cho hai điểm mà đường thẳng đi qua, bạn có thể thay tọa độ của hai điểm này vào phương trình y = ax + b để tìm a và b.
Để tìm giao điểm của hai đường thẳng, bạn cần giải hệ phương trình gồm phương trình của hai đường thẳng đó. Có nhiều phương pháp để giải hệ phương trình, như phương pháp thế, phương pháp cộng đại số, hoặc phương pháp đồ thị. Hãy chọn phương pháp phù hợp nhất với từng bài toán cụ thể.
Để giải quyết bài toán thực tế bằng hàm số bậc nhất, bạn cần thực hiện các bước sau:
Bài toán: Một người đi xe máy từ A đến B với vận tốc 40 km/h. Sau 1 giờ 30 phút, người đó còn cách B 50 km. Tính quãng đường AB.
Lời giải:
Gọi x là thời gian người đó đi từ A đến B (giờ). Quãng đường người đó đi được là 40x (km). Quãng đường còn lại là 50 km. Vậy, quãng đường AB là 40x + 50 (km).
Theo đề bài, sau 1 giờ 30 phút (tức là 1,5 giờ), người đó còn cách B 50 km. Vậy, x = 1,5. Thay x = 1,5 vào biểu thức quãng đường AB, ta được:
Quãng đường AB = 40 * 1,5 + 50 = 60 + 50 = 110 (km).
Bài 1 trang 102 sách bài tập toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải quyết vấn đề. Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể mà chúng tôi đã cung cấp, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả.