Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 1 trang 45 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Một nhà máy tổ chức thi tuyển kĩ thuật viên mới. Thời gian hoàn thành một bài thực hành của các ứng viên được ghi lại ở bảng sau (đơn vị: giây). a) Hãy chia số liệu trên thành 5 nhóm với nhóm đầu tiên là [300; 350). Tìm tần số và tần số tương đối của mỗi nhóm b) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho mẫu số liệu ghép nhóm đó. c) Người ta sẽ loại 40% ứng viên có thời gian hoàn thành bài thi lâu nhất. Hỏi các thí sinh có thời gian hoàn thành bài thi trên bao nhiêu giây
Đề bài
Một nhà máy tổ chức thi tuyển kĩ thuật viên mới. Thời gian hoàn thành một bài thực hành của các ứng viên được ghi lại ở bảng sau (đơn vị: giây).
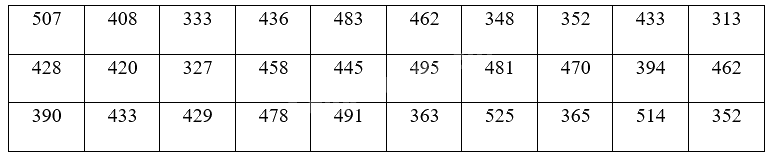
a) Hãy chia số liệu trên thành 5 nhóm với nhóm đầu tiên là [300; 350). Tìm tần số và tần số tương đối của mỗi nhóm
b) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho mẫu số liệu ghép nhóm đó.
c) Người ta sẽ loại 40% ứng viên có thời gian hoàn thành bài thi lâu nhất. Hỏi các thí sinh có thời gian hoàn thành bài thi trên bao nhiêu giây sẽ bị loại?
Phương pháp giải - Xem chi tiết
Dựa vào: Độ rộng của nhóm là 50 để chia thành 5 nhóm. Đếm số lượng các giá trị của mẫu số liệu để tìm tần số. Công thức tần số tương đối của mỗi nhóm là \(f = \frac{m}{N}.100\% \) (m là tần số nhóm, N là cỡ mẫu).
Bảng tần số ghép nhóm có dạng:

Bảng tần số tương đối ghép nhóm có dạng:

Nhìn vào bảng tần số tương đối ghép nhóm để nhận xét.
Lời giải chi tiết
a) Cỡ mẫu N = 30.
Các nhóm số liệu lần lượt là [300; 350); [350; 400); [400; 450); [450; 500); [500; 550).
Tần số tương đối của 5 nhóm trên lần lượt là m1 = 4; m2 = 6; m3 = 8; m4 = 9; m5 = 3.
Gọi \({f_1},{f_2},{f_3},{f_4},{f_5}\) lần lượt là tần số tương đối của các nhóm số liệu trên.
Ta có:
\(\begin{array}{l}{f_1} = \frac{4}{{30}}.100\% = 13,3\% ;{f_2} = \frac{6}{{30}}.100\% = 20\% ;{f_3} = \frac{8}{{30}}.100\% = 26,7\% \\{f_4} = \frac{9}{{30}}.100\% = 30\% ;{f_5} = \frac{3}{{30}}.100\% = 10\% \end{array}\)
b) Bảng tần số ghép nhóm

c) Tần số tương đối của các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên là 30% + 10% = 40%.
Vậy các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên sẽ bị loại.
Bài 1 trang 45 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và đường thẳng song song, vuông góc.
Bài 1 gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 1 trang 45 sách bài tập Toán 9 - Chân trời sáng tạo tập 2, học sinh cần nắm vững các kiến thức sau:
Câu a: Xác định hệ số góc của đường thẳng y = 2x - 3.
Hệ số góc của đường thẳng y = 2x - 3 là a = 2.
Câu b: Tìm m để đường thẳng y = (m - 1)x + 2 song song với đường thẳng y = 3x + 1.
Để hai đường thẳng song song, ta cần có m - 1 = 3 và 2 ≠ 1. Suy ra m = 4.
Câu c: Tìm m để đường thẳng y = (2m + 1)x - 5 vuông góc với đường thẳng y = -x + 3.
Để hai đường thẳng vuông góc, ta cần có (2m + 1) * (-1) = -1. Suy ra 2m + 1 = 1, do đó m = 0.
Giả sử chúng ta có đường thẳng y = -x + 5. Để tìm đường thẳng song song với đường thẳng này, chúng ta cần chọn hệ số góc là -1. Ví dụ, đường thẳng y = -x + 2 là một đường thẳng song song với y = -x + 5.
Để tìm đường thẳng vuông góc với đường thẳng y = -x + 5, chúng ta cần chọn hệ số góc là 1 (vì (-1) * 1 = -1). Ví dụ, đường thẳng y = x + 1 là một đường thẳng vuông góc với y = -x + 5.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 1 trang 45 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các tính chất của nó. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, bạn đã có thể tự tin giải bài tập này và đạt kết quả tốt trong học tập.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b, a ≠ 0 |
| Hệ số góc | a, xác định độ dốc của đường thẳng |
| Đường thẳng song song | a1 = a2, b1 ≠ b2 |
| Đường thẳng vuông góc | a1 * a2 = -1 |