Bài 6 trang 89 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số, đồ thị hàm số và các tính chất của hàm số để tìm ra lời giải chính xác.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 89 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm. a) Tính độ dài đường cao OH của tam giác AOB. b) Chứng minh đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi. c) Tính độ dài các đoạn thẳng AH và BH.
Đề bài
Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm.
a) Tính độ dài đường cao OH của tam giác AOB.
b) Chứng minh đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.
c) Tính độ dài các đoạn thẳng AH và BH.
Phương pháp giải - Xem chi tiết
Dựa vào: Một đường thẳng là tiếp tuyến của đường tròn khi nó đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
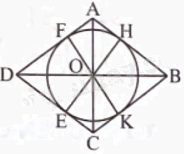
a) Ta có \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{6^2} + {8^2}} = 10(cm).\)
\(2{S_{\Delta AOB}} = OA.OB = OH.AB\)
Suy ra OH = \(\frac{{OA.OB}}{{AB}} = \frac{{6.8}}{{10}} = 4,8(cm)\).
b) Lần lượt vẽ đường cao OK, OE, OF của tam giác BOC, COD, DOA.
Ta có bốn tam giác vuông AOB, AOD, COD, COB bằng nhau (c.g.c), suy ra bốn đường cao OH, OF, OE, OK cũng bằng nhau.
Do khoảng cách từ O đến bốn cạnh của hình thoi đều bằng OH nên đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.
c) Ta có:
\(AH =OA.\cos \widehat {OAB} = OA.\frac{{OA}}{{AB}} = \frac{{O{A^2}}}{{AB}} = \frac{{{6^2}}}{{10}} = 3,6(cm).\)
BH = AB – AH = 10 – 2,6 = 6,4 (cm).
Bài 6 trang 89 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài toán này thường yêu cầu học sinh xác định hàm số, vẽ đồ thị hàm số, hoặc tìm các yếu tố liên quan đến hàm số như hệ số góc, giao điểm với các trục tọa độ. Để giải bài toán này hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài toán. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số bước giải chung:
Giả sử bài toán yêu cầu: Cho hàm số y = 2x - 3. Hãy tìm giao điểm của đồ thị hàm số với trục Ox và trục Oy.
Lời giải:
Ngoài bài 6 trang 89, sách bài tập Toán 9 - Chân trời sáng tạo tập 1 còn có nhiều bài tập tương tự về hàm số bậc nhất. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc nhất và luyện tập thường xuyên. Ngoài ra, việc sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị cũng có thể giúp học sinh giải bài tập nhanh chóng và chính xác hơn.
Khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý một số điều sau:
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 6 trang 89 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 và các bài tập tương tự. Chúc các em học tập tốt!