Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để các em hiểu rõ bản chất của bài toán. Hãy cùng bắt đầu nhé!
Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, CD = (2sqrt 3 ) cm. Tính a) Bán kính đường tròn (O). b) Số đo (widehat {CAB}).
Đề bài
Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, CD = \(2\sqrt 3 \) cm. Tính
a) Bán kính đường tròn (O).
b) Số đo \(\widehat {CAB}\).
Phương pháp giải - Xem chi tiết
Dựa vào: Mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó.
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
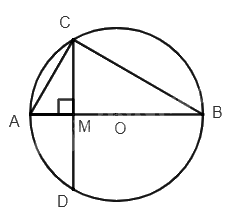
a) Ta có AB là trục đối xứng của đường tròn (O), suy ra MC = MD = \(\frac{{CD}}{2} = \sqrt 3 \) (cm).
Tam giác ABC có CO = OA = OB = R, suy ra ABC là tam giác vuông tại C.
Ta có \(\Delta AMC \backsim \Delta CMB(g.g)\) suy ra \(\frac{{MA}}{{MC}} = \frac{{MC}}{{MB}}\), suy ra \(MB = \frac{{M{C^2}}}{{MA}} = \frac{{\left( {\sqrt 3 } \right){}^2}}{1} = 3(cm)\).
Khi đó AB = MA + MB = 1 + 3 = 4 = 2R, suy ra R = 2 cm.
b) Trong tam giác AMC vuông tại M, ta có:
\(\tan \widehat {CAB} = \frac{{MC}}{{MA}} = \sqrt 3 \), suy ra \(\widehat {CAB} \approx {60^o}\).
Bài 5 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài 5 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 5 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, học sinh cần nắm vững các kiến thức sau:
Để xác định hệ số a của hàm số y = ax + b khi biết một điểm thuộc đồ thị hàm số, ta thay tọa độ của điểm đó vào phương trình hàm số và giải phương trình để tìm a.
Ví dụ: Cho hàm số y = ax + b và điểm A(1; 2) thuộc đồ thị hàm số. Thay x = 1 và y = 2 vào phương trình, ta được: 2 = a * 1 + b. Từ đó, ta có thể giải phương trình để tìm a.
Để tìm giá trị của b khi biết hệ số a và một điểm thuộc đồ thị hàm số, ta thực hiện tương tự như câu a). Thay tọa độ của điểm và giá trị của a vào phương trình hàm số và giải phương trình để tìm b.
Để viết phương trình đường thẳng đi qua hai điểm cho trước, ta có thể sử dụng công thức tính hệ số góc và phương trình đường thẳng.
Công thức tính hệ số góc m của đường thẳng đi qua hai điểm A(x1; y1) và B(x2; y2) là: m = (y2 - y1) / (x2 - x1).
Phương trình đường thẳng đi qua điểm A(x1; y1) và có hệ số góc m là: y - y1 = m(x - x1).
Các bài toán ứng dụng liên quan đến hàm số bậc nhất thường yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các vấn đề thực tế. Ví dụ, bài toán về quãng đường đi được của một vật chuyển động đều, bài toán về tiền lương của một người lao động, v.v.
Bài 5 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn khi làm bài tập Toán 9.
Chúc các em học tập tốt!