Giải bài 18 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1

Giải bài 18 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Giải bài 18 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1

Bài 18 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 18 trang 75, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Một người đứng trên một tháp hải đăng ở vị trí cao 75 m so với mặt nước biển đã quan sát hai lần thấy một chiếc thuyền đang hướng về phía tháp hải đăng với góc hạ lần lượt là 30o và 45o (Hình 10). Hỏi thuyền đi được bao nhiêu mét giữa hai lần quan sát?

Đề bài

Một người đứng trên một tháp hải đăng ở vị trí cao 75 m so với mặt nước biển đã quan sát hai lần thấy một chiếc thuyền đang hướng về phía tháp hải đăng với góc hạ lần lượt là 30^o và 45^o (Hình 10). Hỏi thuyền đi được bao nhiêu mét giữa hai lần quan sát?

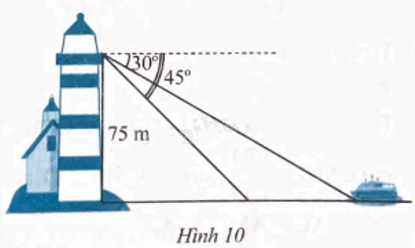
Giải bài 18 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1 1

Phương pháp giải - Xem chi tiết Giải bài 18 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1 2

Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.

Lời giải chi tiết

Gọi độ cao từ mắt người đó đến mặt nước biển là AB, suy ra AB = 75 m.

Gọi vị trí chiếc thuyền hướng về ngọn hải đăng mà từ trên ngọn tháp quan sát với góc hạ lần lượt là 30^o và 45^o lần lượt là C, D.

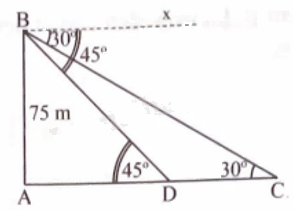
Giải bài 18 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1 3

Vì Bx // AD nên \(\left\{ {\begin{array}{*{20}{c}}{\widehat {xBD} = \widehat {BDA} = {{45}^o}}\\{\widehat {xBC} = \widehat {BCA} = {{30}^o}}\end{array}} \right.\) (hai góc so le trong).

Xét \(\Delta ABD\) vuông tại A, ta có \(\widehat {BDA} = {45^o}\), suy ra \(\Delta ABD\) vuông cân tại A.

Suy ra AB = AD = 75 m.

Xét \(\Delta ABC\) vuông tại A, ta có AC = AB. cot \(\widehat {BCA} = 75.\cot {30^o}\), suy ra AC = \(75\sqrt 3 \approx 129,90(m).\)

DC = AC – AD = \(75\sqrt 3 \approx 129,90 - 75 = 54,90(m).\)

Vậy giữa hai lần quan sát, thuyền đi được khoảng 54,90 m.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 18 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1 đặc sắc thuộc chuyên mục toán lớp 9 trên nền tảng học toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 18 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1: Hướng dẫn chi tiết

Bài 18 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học Toán 9, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như các phương pháp vẽ đồ thị hàm số.

Nội dung bài tập

Bài 18 trang 75 thường bao gồm các dạng bài tập sau:

Xác định hàm số: Cho các thông tin về đồ thị hoặc các điểm thuộc đồ thị, yêu cầu xác định hàm số.
Tìm hệ số góc và tung độ gốc: Cho hàm số, yêu cầu tìm hệ số góc và tung độ gốc.
Vẽ đồ thị hàm số: Cho hàm số, yêu cầu vẽ đồ thị hàm số trên mặt phẳng tọa độ.
Ứng dụng hàm số vào giải quyết bài toán thực tế: Các bài toán liên quan đến việc mô tả mối quan hệ giữa các đại lượng bằng hàm số.

Hướng dẫn giải chi tiết

Để giải bài 18 trang 75 một cách hiệu quả, bạn có thể tham khảo các bước sau:

Đọc kỹ đề bài: Xác định rõ yêu cầu của bài tập và các thông tin đã cho.
Xác định hàm số: Nếu bài tập yêu cầu xác định hàm số, hãy sử dụng các thông tin đã cho để tìm hệ số góc và tung độ gốc.
Vẽ đồ thị hàm số: Nếu bài tập yêu cầu vẽ đồ thị hàm số, hãy chọn các điểm thuộc đồ thị và nối chúng lại với nhau.
Ứng dụng hàm số vào giải quyết bài toán thực tế: Nếu bài tập là bài toán thực tế, hãy mô tả mối quan hệ giữa các đại lượng bằng hàm số và giải phương trình để tìm ra kết quả.

Ví dụ minh họa

Bài tập: Cho hàm số y = 2x + 1. Hãy vẽ đồ thị hàm số này.

Giải:

Xác định các điểm thuộc đồ thị: Chọn x = 0, ta có y = 1. Chọn x = 1, ta có y = 3. Vậy, hai điểm A(0; 1) và B(1; 3) thuộc đồ thị hàm số.
Vẽ đồ thị: Vẽ mặt phẳng tọa độ Oxy. Đánh dấu hai điểm A(0; 1) và B(1; 3) lên mặt phẳng tọa độ. Nối hai điểm A và B lại với nhau, ta được đồ thị hàm số y = 2x + 1.

Lưu ý quan trọng

Khi giải bài tập về hàm số, bạn cần lưu ý những điều sau:

Nắm vững các khái niệm cơ bản về hàm số.
Hiểu rõ cách xác định hệ số góc và tung độ gốc.
Biết cách vẽ đồ thị hàm số.
Rèn luyện kỹ năng giải quyết các bài toán thực tế.

Mở rộng kiến thức

Để hiểu sâu hơn về hàm số, bạn có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 9.
Sách bài tập Toán 9.
Các trang web học Toán online uy tín.

Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 18 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 và đạt kết quả tốt trong môn Toán.

Việc nắm vững kiến thức về hàm số không chỉ giúp các em giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng quan trọng cho việc học tập các môn học khác liên quan đến Toán học. Hãy dành thời gian ôn tập và thực hành thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán.

Ngoài ra, các em có thể tìm kiếm thêm các bài tập tương tự trên Giaitoan.edu.vn để rèn luyện thêm. Chúng tôi luôn cập nhật những lời giải chi tiết và dễ hiểu nhất để giúp các em học tập hiệu quả.