Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 8 trang 69 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em học sinh hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, chính xác và dễ hiểu nhất để hỗ trợ các em trong quá trình học tập môn Toán.
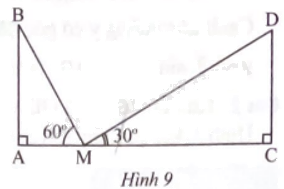
Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m). Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là 60o và 30o. Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.
Đề bài
Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m). Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là 60o và 30o. Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.
Phương pháp giải - Xem chi tiết
Sử dụng tỉ số lượng giác trong tam giác vuông để tính.
Lời giải chi tiết
Xét tam giác ABM vuông tại A, ta có: \(\cot \widehat {AMB} = \frac{{AM}}{{AB}}\), suy ra AM = AB. \(\cot \widehat {AMB}\).
Xét tam giác CMD vuông tại C, ta có: \(\cot \widehat {CMB} = \frac{{CM}}{{CD}}\), suy ra CM = CD. \(\cot \widehat {CMB}\)
= AB. \(\cot \widehat {CMB}\).
Ta có AC = AM + CM
80 = AB. cot 60o + AB. cot 30o
80 = AB (cot 60o + cot 30o)
AB = \(\frac{{80}}{{\cot {{60}^o} + \cot {{30}^o}}} = 20\sqrt 3 \).
Khoảng cách từ điểm M đến trụ điện AB là:
\(AM = AB.\cot \widehat {AMB} = 20\sqrt 3 .\frac{{\sqrt 3 }}{3} = 20(m).\)
Khoảng cách từ điểm M đến trụ điện CD là:
MC = AC – AM = 80 – 20 = 60 (m).
Bài 8 trang 69 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, biểu đồ và ứng dụng của hàm số trong đời sống.
Bài 8 bao gồm các dạng bài tập sau:
Cho hàm số y = 2x - 3. Tính giá trị của y khi x = -1; x = 0; x = 2.
Giải:
Vẽ đồ thị của hàm số y = -x + 2.
Giải:
Để vẽ đồ thị của hàm số y = -x + 2, ta xác định hai điểm thuộc đồ thị:
Nối hai điểm A và B lại, ta được đồ thị của hàm số y = -x + 2.
Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải:
Để tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3, ta giải hệ phương trình:
{ y = x + 1y = -x + 3 }
Từ hai phương trình trên, ta có:
x + 1 = -x + 3
2x = 2
x = 1
Thay x = 1 vào phương trình y = x + 1, ta được:
y = 1 + 1 = 2
Vậy giao điểm của hai đường thẳng y = x + 1 và y = -x + 3 là điểm (1; 2).
Bài 8 trang 69 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán.