Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 49 sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về bài học.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Bảng sau ghi lại số bàn thắng mà câu lạc bộ bóng đá ABC đã ghi được trong mỗi trận đấu sau một mùa giải. a) Trong mùa giải nói trên, câu lạc bộ ABC đã thi đấu bao nhiêu trận? b) Số bàn thắng câu lạc bộ ABC ghi được trong mỗi trận đấu nhận những giá trị nào? Xác định tần số của mỗi giá trị đó. c) Lập bảng tần số tương đối và vẽ biểu đồ hình quạt tròn biểu diễn mẫu số liệu nói trên (kết quả làm tròn đến hàng phần mười).
Đề bài
Bảng sau ghi lại số bàn thắng mà câu lạc bộ bóng đá ABC đã ghi được trong mỗi trận đấu sau một mùa giải.

a) Trong mùa giải nói trên, câu lạc bộ ABC đã thi đấu bao nhiêu trận?
b) Số bàn thắng câu lạc bộ ABC ghi được trong mỗi trận đấu nhận những giá trị nào? Xác định tần số của mỗi giá trị đó.
c) Lập bảng tần số tương đối và vẽ biểu đồ hình quạt tròn biểu diễn mẫu số liệu nói trên (kết quả làm tròn đến hàng phần mười).
Phương pháp giải - Xem chi tiết
Nhìn vào bảng và đếm số giá trị khác nhau và số lần xuất hiện của mỗi giá trị.
Bảng tần số tương đối:

Biểu đồ tần số tương đối dạng hình quạt tròn được biểu thị tần số tương đối a% có số đo cung tương ứng là a%.360o = 3,6ao.
Lời giải chi tiết
a) Trong mùa giải nói trên, câu lạc bộ ABC đã thi đấu 26 trận.
b) Số bàn thắng câu lạc bộ ABC ghi được trong mỗi trận đấu nhận các giá trị 0; 1; 2; 3; 4. Tần số của các giá trị này lần lượt là 6; 9; 7; 3; 1.
c) Gọi \({f_1},{f_2},{f_3},{f_4},{f_5}\) lần lượt là tần số tương đối của các giá trị 0; 1; 2; 3; 4. Ta có:
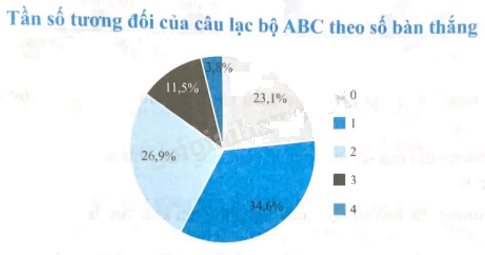
\(\begin{array}{l}{f_1} = \frac{6}{{26}}.100\% = 23,1\% ,{f_2} = \frac{9}{{26}}.100\% = 34,6\% ,{f_3} = \frac{7}{{26}}.100\% = 26,9\% ,\\{f_4} = \frac{3}{{26}}.100\% = 11,5\% ,{f_5} = \frac{1}{{26}}.100\% = 3,8\% \end{array}\)
Bảng tần số tương đối:
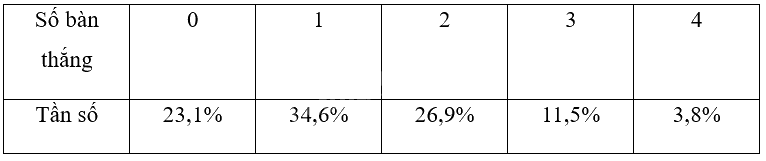
Số đo cung tròn tương ứng với các hình quạt tròn biểu diễn tần số tương đối của các giá trị như sau:
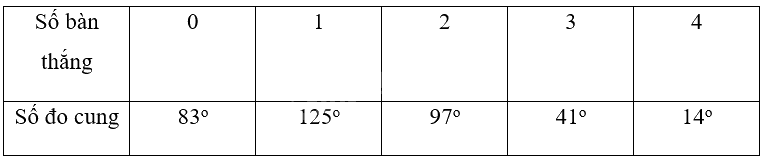
Biểu đồ tần số tương đối hình quạt tròn:
Bài 6 trang 49 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, rèn luyện kỹ năng phân tích và giải quyết vấn đề.
Bài 6 bao gồm các dạng bài tập sau:
Để giải câu a, ta cần xác định hệ số góc và tung độ gốc của hàm số. Hàm số có dạng y = ax + b. Để tìm a và b, ta có thể sử dụng các điểm thuộc đồ thị hàm số hoặc các thông tin khác được cung cấp trong đề bài.
Ví dụ, nếu đồ thị hàm số đi qua hai điểm A(x1, y1) và B(x2, y2), ta có thể tính a bằng công thức: a = (y2 - y1) / (x2 - x1). Sau khi tìm được a, ta có thể tìm b bằng cách thay tọa độ của một trong hai điểm A hoặc B vào phương trình y = ax + b.
Để tìm điểm thuộc đồ thị hàm số, ta có thể thay giá trị x vào phương trình hàm số và tính giá trị y tương ứng. Ví dụ, nếu x = 2, ta có y = a * 2 + b. Điểm (2, y) sẽ là một điểm thuộc đồ thị hàm số.
Để vẽ đồ thị hàm số, ta cần xác định ít nhất hai điểm thuộc đồ thị hàm số. Sau đó, ta vẽ đường thẳng đi qua hai điểm này. Đường thẳng này chính là đồ thị của hàm số.
Các bài toán ứng dụng liên quan đến hàm số bậc nhất thường yêu cầu học sinh sử dụng kiến thức về hàm số để mô tả và giải quyết các tình huống thực tế. Ví dụ, bài toán có thể yêu cầu tính quãng đường đi được của một vật chuyển động đều với vận tốc không đổi, hoặc tính số tiền lãi khi đầu tư với lãi suất cố định.
Để củng cố kiến thức và kỹ năng, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 2 và các tài liệu học tập khác.
Bài 6 trang 49 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập tương tự.