Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 13 trang 89 sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 9 nhé!
Cho tam giác ABC có (O) là đường tròn ngoại tiếp. Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn (O). Biết AB = 8 cm; AC = 15 cm và AH = 5 cm. a) Chứng minh (Delta AHBbacksim Delta ACD). b) Tính độ dài bán kính của đường tròn
Đề bài
Cho tam giác ABC có (O) là đường tròn ngoại tiếp. Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn (O). Biết AB = 8 cm; AC = 15 cm và AH = 5 cm.
a) Chứng minh \(\Delta AHB\backsim \Delta ACD\).
b) Tính độ dài bán kính của đường tròn
Phương pháp giải - Xem chi tiết
Chứng minh theo trường hợp góc – góc.
Từ chứng minh phần a suy ra tỉ số đồng dạng và tìm bán kính của đường tròn.
Lời giải chi tiết
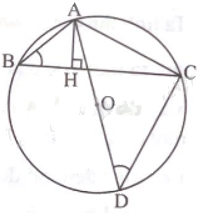
a) Ta có \(\widehat {ACD}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACD} = {90^o}\).
Xét \(\Delta AHB\) và \(\Delta ACD\) có
\(\widehat {AHB} = \widehat {ACD} = {90^o}\)
\(\widehat {ABH} = \widehat {ADC}\)(hai góc nội tiếp cùng chắn cung AC).
Do đó \(\Delta AHB\backsim \Delta ACD\) (g.g).
b) Vì \(\Delta AHB\backsim \Delta ACD\) nên \(\frac{{AH}}{{AC}} = \frac{{AB}}{{AD}}\) hay AH.AD = AB.AC, suy ra AD = \(\frac{{8.15}}{5} = 24\) (cm).
Do đó độ dài bán kính của đường tròn (O) là \(\frac{{24}}{2} = 12\) (cm).
Bài 13 trang 89 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, liên quan đến việc xác định hệ số góc, đường thẳng song song, và ứng dụng hàm số vào các bài toán hình học.
Bài 13 bao gồm các câu hỏi và bài tập sau:
Để xác định hệ số góc của đường thẳng có phương trình y = ax + b, ta chỉ cần xác định giá trị của a. Nếu phương trình đường thẳng được cho dưới dạng tổng quát Ax + By + C = 0, ta có thể chuyển về dạng y = ax + b để xác định hệ số góc.
Ví dụ: Cho đường thẳng 2x + 3y - 6 = 0. Ta chuyển về dạng y = (-2/3)x + 2. Vậy hệ số góc của đường thẳng là -2/3.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song khi và chỉ khi a1 = a2 và b1 ≠ b2. Điều này có nghĩa là hai đường thẳng phải có cùng hệ số góc nhưng khác hệ số tự do.
Ví dụ: Đường thẳng y = 2x + 1 và y = 2x - 3 song song với nhau vì chúng có cùng hệ số góc là 2 nhưng khác hệ số tự do.
Để xác định phương trình đường thẳng đi qua hai điểm M(x1; y1) và N(x2; y2), ta thực hiện các bước sau:
Ví dụ: Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4).
Các bài toán ứng dụng thường yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để mô tả mối quan hệ giữa các đại lượng trong thực tế. Để giải các bài toán này, ta cần:
Bài 13 trang 89 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.