Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp cho các em đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài tập này nhé!
Cho đường tròn (O; 8 cm) và hai điểm A, B nằm trên đường tròn thoả mãn AB = 6 cm. Vẽ đường kính MN sao cho hai đoạn thẳng MN và AB không có điểm chung. Gọi A’, B’ lần lượt là hai điểm đối xứng với A, B qua MN. Chứng minh: a) ABB’A’ là hình thang cân. b) Bốn điểm A, B, B’, A’ cùng nằm trên đường tròn (O; 8 cm).
Đề bài
Cho đường tròn (O; 8 cm) và hai điểm A, B nằm trên đường tròn thoả mãn AB = 6 cm. Vẽ đường kính MN sao cho hai đoạn thẳng MN và AB không có điểm chung. Gọi A’, B’ lần lượt là hai điểm đối xứng với A, B qua MN. Chứng minh:
a) ABB’A’ là hình thang cân.
b) Bốn điểm A, B, B’, A’ cùng nằm trên đường tròn (O; 8 cm).
Phương pháp giải - Xem chi tiết
Dựa vào: Đường tròn tâm O bán kính R (R > 0) là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.
Mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó.
Lời giải chi tiết
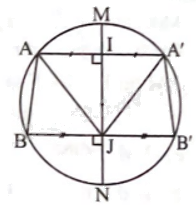
a) Ta có AA’ // BB’ (Vì cùng vuông góc với MN) (1)
Gọi I, J lần lượt là giao điểm của MN với AA’, BB’. Ta có \(\Delta AIJ = \Delta A'IJ\), suy ra AJ = A’J, suy ra \(\Delta ABJ = \Delta A'B'J\), suy ra \(\widehat B = \widehat {B'}\). (2)
Từ (1) và (2), suy ra ABB’A’ là hình thang cân.
b) Ta có MN là trục đối xứng của đường tròn (O; 8 cm), A, B đã thuộc đường tròn (O; 8 cm) suy ra A’, B’ là hai điểm đối xứng với A, B qua MN nên cũng thuộc đường tròn (O; 8 cm), suy ra bốn điểm A, B, A’, B’ cùng nằm trên đường tròn (O; 8 cm).
Bài 4 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài 4 bao gồm các ý nhỏ khác nhau, mỗi ý yêu cầu học sinh thực hiện một thao tác cụ thể liên quan đến hàm số bậc nhất. Các ý thường xoay quanh việc:
Để giải bài 4 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng ý của bài 4 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1:
Để xác định hệ số a, ta thay tọa độ của điểm thuộc đồ thị hàm số vào phương trình y = ax + b. Sau đó, giải phương trình để tìm ra giá trị của a.
Ví dụ: Nếu đồ thị hàm số đi qua điểm (1; 2), ta có: 2 = a * 1 + b. Từ đó, ta có thể giải phương trình để tìm ra giá trị của a.
Để tính giá trị của y, ta thay giá trị của x vào phương trình y = ax + b. Sau đó, thực hiện các phép tính để tìm ra giá trị của y.
Ví dụ: Nếu x = 3 và y = 2x + 1, ta có: y = 2 * 3 + 1 = 7.
Hệ số a trong hàm số y = ax + b cho biết độ dốc của đường thẳng. Nếu a > 0, đường thẳng đồng biến (tăng khi x tăng). Nếu a < 0, đường thẳng nghịch biến (giảm khi x tăng). Độ lớn của a cho biết mức độ dốc của đường thẳng.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập tương tự sau:
Bài 4 trang 85 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất. Hy vọng rằng, với lời giải chi tiết và phương pháp giải rõ ràng mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn khi giải các bài tập tương tự.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hệ số a | Độ dốc của đường thẳng |