Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 66 sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để các em hiểu rõ bản chất của bài toán.
Kết quả kiểm tra tình trạng cân nặng của các học sinh lớp 9B được thống kê lại ở bảng sau: Chọn ngẫu nhiên 1 học sinh lớp 9B. Tính xác suất của mỗi biến cố sau: A: “Học sinh được chọn là học sinh nữ và có cân nặng bình thường”; B: “Học sinh được chọn bị thừa cân”; C: “Học sinh được chọn là học sinh nam”.
Đề bài
Kết quả kiểm tra tình trạng cân nặng của các học sinh lớp 9B được thống kê lại ở bảng sau:
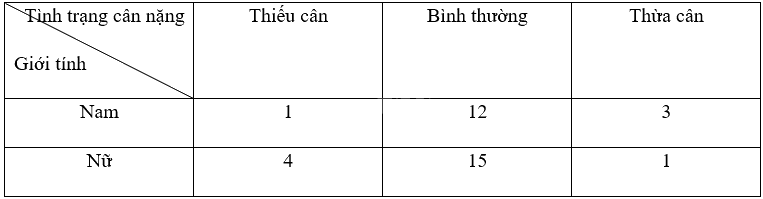
Chọn ngẫu nhiên 1 học sinh lớp 9B. Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là học sinh nữ và có cân nặng bình thường”;
B: “Học sinh được chọn bị thừa cân”;
C: “Học sinh được chọn là học sinh nam”.
Phương pháp giải - Xem chi tiết
Trong phép thử ngẫu nhiên, hai kết quả đồng khả năng nếu chúng có khả năng xảy ra như nhau.
Xác suất của biến cố A được tính bởi công thức:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}}\), trong đó n(A) là số kết quả thuận lợi cho A; \(n(\Omega )\) là số các kết quả có thể xảy ra.
Lời giải chi tiết
Tổng số học sinh là 1 + 12 + 3 + 4 + 15 + 1 = 36 (học sinh).
Số các kết quả có thể xảy ra là \(n(\Omega ) = 36\).
Số học sinh nữ có cân nặng bình thường là 15 nên số kết quả thuận lợi cho biến cố A là n(A) = 15.
Xác suất của biến cố A là P(A) = \(\frac{{15}}{{36}} = \frac{5}{{12}}\).
Số học sinh bị thừa cân là 3 + 1 = 4 (học sinh).
Số kết quả thuận lợi cho biến cố B là n(B) = 4
Xác suất của biến cố B là \(P(B) = \frac{4}{{36}} = \frac{1}{9}\).
Số học sinh nam 1 + 12 + 3 = 16 (học sinh).
Số kết quả thuận lợi cho biến cố C là n(C) = 16.
Xác suất của biến cố C là P(C) = \(\frac{{16}}{{36}} = \frac{4}{9}\).
Bài 6 trang 66 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như hệ số góc, giao điểm của đồ thị hàm số, và điều kiện để hàm số đồng biến, nghịch biến.
Bài 6 bao gồm các dạng bài tập sau:
Cho hàm số y = 2x + 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Giải:
Hàm số y = 2x + 3 là hàm số bậc nhất có dạng y = ax + b. Trong đó:
Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải:
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình:
Thay phương trình (1) vào phương trình (2), ta được:
x + 1 = -x + 3
2x = 2
x = 1
Thay x = 1 vào phương trình (1), ta được:
y = 1 + 1 = 2
Vậy giao điểm của hai đường thẳng là (1; 2).
Hàm số y = -3x + 2 có đồng biến hay nghịch biến?
Giải:
Hàm số y = -3x + 2 là hàm số bậc nhất có hệ số góc a = -3. Vì a < 0 nên hàm số nghịch biến.
Sách giáo khoa Toán 9 - Chân trời sáng tạo tập 2
Sách bài tập Toán 9 - Chân trời sáng tạo tập 2
Các trang web học Toán online uy tín
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ hiểu rõ hơn về bài 6 trang 66 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 và có thể tự tin giải quyết các bài tập tương tự. Chúc các em học tập tốt!