Bài 2 trang 97 sách bài tập toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 97 sách bài tập toán 9 Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
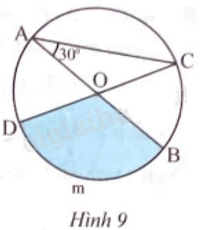
Cho đường tròn (O) đường kính AB = 3 cm, (widehat {CAB}) = 30o (Hình 9). a) Tính độ dài cung BmD. b) Tính diện tích hình quạt tròn OBmD.
Đề bài
Cho đường tròn (O) đường kính AB = 3 cm, \(\widehat {CAB}\) = 30o (Hình 9).
a) Tính độ dài cung BmD.
b) Tính diện tích hình quạt tròn OBmD.
Phương pháp giải - Xem chi tiết
Dựa vào: Trên đường tròn bán kính R, độ dài l của một cung có số đo no được tính theo công thức \(l = \frac{{\pi Rn}}{{180}}\).
Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết
a) Ta có \(\widehat {DOB} = {180^o} - 2.\widehat {CAB} = {120^o}\)
Suy ra \({{l}_{\overset\frown{BmD}}}=\frac{\pi .1,5.120}{180}=\pi \approx 3,14(cm).\)
b) \({S_{OBmD}} = \frac{{\pi {{.1,5}^2}.120}}{{180}} = \frac{3}{4}\pi \approx 2,36(c{m^2}).\)
Bài 2 trang 97 sách bài tập toán 9 Chân trời sáng tạo tập 1 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc xác định phương trình đường thẳng song song và ứng dụng hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Bài 2 cụ thể yêu cầu gì? (Nội dung bài tập sẽ được chèn vào đây, ví dụ: Cho hai đường thẳng y = 2x + 1 và y = 2x - 3. Hãy chứng minh hai đường thẳng này song song.)
Để giải bài tập này, chúng ta thực hiện các bước sau:
Xét hai đường thẳng y = -3x + 5 và y = -3x + 2. Tương tự như trên, ta có a1 = a2 = -3 và b1 = 5 ≠ b2 = 2. Vậy hai đường thẳng này cũng song song với nhau.
Khi giải các bài toán liên quan đến đường thẳng song song, cần chú ý đến cả hai điều kiện: cùng hệ số góc và khác tung độ gốc. Nếu chỉ một trong hai điều kiện được thỏa mãn, hai đường thẳng không song song.
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Kiến thức về hàm số bậc nhất và đường thẳng song song có ứng dụng rộng rãi trong thực tế, ví dụ như trong việc mô tả quỹ đạo của vật chuyển động, thiết kế các công trình xây dựng, hoặc phân tích các dữ liệu kinh tế.
Bài 2 trang 97 sách bài tập toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và đường thẳng song song. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
| Đường thẳng | Hệ số góc (a) | Tung độ gốc (b) |
|---|---|---|
| y = 2x + 1 | 2 | 1 |
| y = 2x - 3 | 2 | -3 |