Giải bài 14 trang 100 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1

Giải bài 14 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Giải bài 14 trang 100 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1

Bài 14 trang 100 sách bài tập Toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc, vẽ đồ thị hàm số và ứng dụng vào giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 14 trang 100, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (D thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh: a) MA.MB = MC.MD. b) Tứ giác ABEC là hình thang cân. c) Tổng MA2 + MB2 + MC2 + MD2 có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Đề bài

Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (D thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh:

a) MA.MB = MC.MD.

b) Tứ giác ABEC là hình thang cân.

c) Tổng MA² + MB² + MC² + MD² có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Phương pháp giải - Xem chi tiết Giải bài 14 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1 1

Dựa vào: Hai góc nội tiếp cùng chắn một cung thì bằng nhau.

Chứng minh ABEC là hình thang. Sau đó chứng minh \(\widehat {EBA} = \widehat {CAB}\) để ABEC là hình thang cân.

Chứng minh tổng MA² + MB² + MC² + MD² theo R.

Lời giải chi tiết

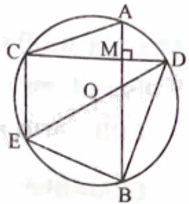
Giải bài 14 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1 2

a) Xét \(\Delta \)MAC và \(\Delta \)MDB, ta có \(\widehat{AMC}=\widehat{DMB}={{90}^{o}},\widehat{ACM}=\widehat{DBM}\left( \frac{1}{2}sđ\overset\frown{AD} \right).\)

Do đó \(\Delta \)MAC \(\backsim \) \(\Delta \)MDB, suy ra \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MB}}\) hay MA.MB = MC.MD.

b) Vì DE là đường kính nên ta có \(CE \bot CD\).

Mà \(AB \bot CD\) nên AB // CE, suy ra ABEC là hình thang.

Ta có \(\widehat {EBA} + \widehat {DBM} = {90^o};\widehat {CAB} + \widehat {ACM} = {90^o};\widehat{ACM}=\widehat{DBM}\), suy ra \(\widehat {EBA} = \widehat {CAB}\). Vậy ABEC là hình thang cân.

c) Ta có AC = BE (vì ABEC là hình thang cân) và \(\Delta DBE\)vuông tại B, nên ta có

MA² + MB² + MC² + MD² = AC² + BD² = BE² + BD² = ED² = 4R².

Vậy tổng MA² + MB² + MC² + MD² có giá trị không đổi.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 14 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1 đặc sắc thuộc chuyên mục sgk toán 9 trên nền tảng đề thi toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 14 trang 100 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1: Chi tiết và Dễ hiểu

Bài 14 trang 100 sách bài tập Toán 9 Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến đồ thị hàm số và ứng dụng thực tế.

Nội dung bài tập 14 trang 100

Bài tập 14 thường bao gồm các yêu cầu sau:

Xác định hệ số góc của hàm số.
Vẽ đồ thị hàm số.
Tìm tọa độ giao điểm của đồ thị hàm số với các đường thẳng khác.
Giải các bài toán thực tế liên quan đến hàm số bậc nhất.

Lời giải chi tiết bài 14 trang 100

Để giải bài 14 trang 100 sách bài tập Toán 9 Chân trời sáng tạo tập 1, chúng ta cần thực hiện các bước sau:

Bước 1: Xác định hàm số bậc nhất. Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
Bước 2: Xác định hệ số góc a. Hệ số góc a cho biết độ dốc của đường thẳng.
Bước 3: Vẽ đồ thị hàm số. Để vẽ đồ thị hàm số, ta cần xác định ít nhất hai điểm thuộc đồ thị.
Bước 4: Giải các bài toán liên quan đến đồ thị hàm số.

Ví dụ minh họa

Giả sử chúng ta có hàm số y = 2x + 1. Để vẽ đồ thị hàm số này, ta có thể xác định hai điểm A(0; 1) và B(1; 3). Nối hai điểm A và B, ta được đồ thị hàm số y = 2x + 1.

Lưu ý quan trọng

Khi giải bài tập về hàm số bậc nhất, cần lưu ý các điểm sau:

Hệ số góc a quyết định độ dốc của đường thẳng. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải.
Tung độ gốc b là giao điểm của đường thẳng với trục Oy.
Đồ thị hàm số bậc nhất là một đường thẳng.

Ứng dụng của hàm số bậc nhất

Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:

Tính quãng đường đi được của một vật chuyển động đều.
Tính tiền lương của một người lao động theo thời gian làm việc.
Dự báo doanh thu của một công ty.

Bài tập luyện tập

Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập sau:

Bài 15 trang 100 sách bài tập Toán 9 Chân trời sáng tạo tập 1.
Bài 16 trang 100 sách bài tập Toán 9 Chân trời sáng tạo tập 1.

Kết luận

Bài 14 trang 100 sách bài tập Toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh nắm vững kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin giải các bài tập tương tự và đạt kết quả tốt trong môn Toán.