Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 13 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh. Hãy cùng theo dõi và học tập nhé!
Cho tam giác ABC vuông tại A có đường cao AH, BH = 1 cm, CH = 4 cm. Giải tam giác ABC.
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH, BH = 1 cm, CH = 4 cm. Giải tam giác ABC.
Phương pháp giải - Xem chi tiết
Giải tam giác vuông là tính các cạnh và các góc chưa biết của tam giác đó.
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
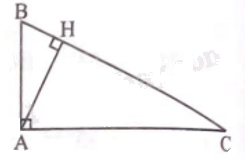
Ta có BC = BH + CH = 1 + 4 = 5 (cm).
Do \(\Delta ABH \backsim \Delta CBA(g.g)\) nên \(\frac{{AB}}{{BH}} = \frac{{BC}}{{AB}}\) hay AB2 = BH.BC = 1.5 = 5, suy ra AB = \(\sqrt 5 \) (cm);
Tương tự, ta có \(\Delta CAH \backsim \Delta CBA(g.g)\) nên \(\frac{{AC}}{{BC}} = \frac{{CH}}{{AC}}\) hay AC2 = CH. BC = 4. 5 = 20, suy ra \(AC = 2\sqrt 5 (cm)\);
sin C = \(\frac{{AB}}{{BC}} = \frac{{\sqrt 5 }}{5}\), suy ra \(\widehat C \approx {26^o}34'\). Suy ra \(\widehat B \approx {63^o}26'\).
Bài 13 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài 13 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 13 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 13 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1:
Để xác định hệ số a của hàm số y = ax + b khi biết một điểm thuộc đồ thị hàm số, ta thay tọa độ của điểm đó vào phương trình hàm số và giải phương trình để tìm a.
Ví dụ: Nếu điểm A(x0; y0) thuộc đồ thị hàm số y = ax + b, thì ta có: y0 = ax0 + b. Từ đó, ta có thể giải phương trình để tìm a.
Để tìm giá trị của b khi biết hệ số a và một điểm thuộc đồ thị hàm số, ta thay tọa độ của điểm đó và giá trị của a vào phương trình hàm số và giải phương trình để tìm b.
Ví dụ: Nếu điểm A(x0; y0) thuộc đồ thị hàm số y = ax + b và a đã biết, thì ta có: y0 = ax0 + b. Từ đó, ta có thể giải phương trình để tìm b.
Để viết phương trình đường thẳng đi qua hai điểm cho trước, ta có thể sử dụng công thức tính hệ số góc và phương trình đường thẳng.
Công thức tính hệ số góc m của đường thẳng đi qua hai điểm A(x1; y1) và B(x2; y2) là: m = (y2 - y1) / (x2 - x1).
Phương trình đường thẳng đi qua điểm A(x1; y1) và có hệ số góc m là: y - y1 = m(x - x1).
Các bài toán ứng dụng liên quan đến hàm số bậc nhất thường yêu cầu học sinh xây dựng mô hình toán học dựa trên các thông tin được cung cấp trong bài toán, sau đó giải phương trình hoặc hệ phương trình để tìm ra kết quả.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về hàm số bậc nhất, học sinh có thể tham khảo các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 và các tài liệu học tập khác.
Bài 13 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, học sinh sẽ tự tin hơn khi giải các bài tập tương tự.