Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 11 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
Tam giác ABC vuông tại A, có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5). a) AC = 8 cm b) (widehat B approx {16,26^o}) c) ({rm{cosC = }}frac{{24}}{{25}}) D. (AH approx 7)
Đề bài
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Tam giác ABC vuông tại A, có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5).
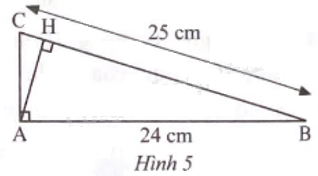
a) AC = 8 cm
b) \(\widehat B \approx {16,26^o}\)
c) \({\rm{cosC = }}\frac{{24}}{{25}}\)
D. \(AH \approx 7\)
Phương pháp giải - Xem chi tiết
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
a) Sai vì AC = \(\sqrt {B{C^2} - A{B^2}} = \sqrt {{{25}^2} - {{24}^2}} = 7\).
b) Đúng vì \(\tan B = \frac{{AC}}{{AB}} = \frac{7}{{24}}\) suy ra \(\widehat B \approx {16,26^o}\).
c) Sai vì \({\rm{cosC = }}\frac{{AC}}{{BC}} = \frac{7}{{25}}\).
d) Đúng vì AH = tan B. AB = \(\frac{7}{{24}}.\)24 = 7 cm.
Bài 11 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song, vuông góc.
Bài 11 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 11 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, học sinh cần nắm vững các kiến thức sau:
Câu a: Xác định hệ số góc của đường thẳng y = 3x - 2.
Hệ số góc của đường thẳng y = 3x - 2 là 3.
Câu b: Tìm m để đường thẳng y = (m - 1)x + 3 song song với đường thẳng y = 2x + 1.
Để hai đường thẳng song song, ta cần có m - 1 = 2 và 3 ≠ 1. Suy ra m = 3.
Câu c: Tìm m để đường thẳng y = (2m + 1)x - 5 vuông góc với đường thẳng y = -x + 2.
Để hai đường thẳng vuông góc, ta cần có (2m + 1) * (-1) = -1. Suy ra 2m + 1 = 1, do đó m = 0.
Bài tập: Viết phương trình đường thẳng đi qua điểm A(1; 2) và song song với đường thẳng y = -2x + 3.
Giải:
Vì đường thẳng cần tìm song song với đường thẳng y = -2x + 3 nên nó có dạng y = -2x + b.
Thay tọa độ điểm A(1; 2) vào phương trình, ta có: 2 = -2 * 1 + b, suy ra b = 4.
Vậy phương trình đường thẳng cần tìm là y = -2x + 4.
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Ngoài ra, các em có thể tham khảo các bài giảng trực tuyến và các tài liệu học tập khác để hiểu rõ hơn về hàm số bậc nhất.
Bài 11 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng, các em sẽ tự tin hơn trong quá trình học tập.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b, a ≠ 0 |
| Hệ số góc | a, xác định độ dốc của đường thẳng |
| Đường thẳng song song | a1 = a2, b1 ≠ b2 |
| Đường thẳng vuông góc | a1 * a2 = -1 |