Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 5 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
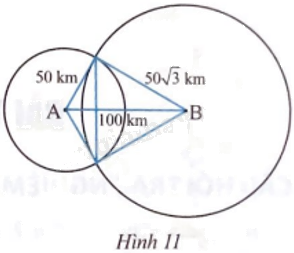
Hai trạm phát sóng A và B đặt cách nhau 100 km. Trạm phát sóng A và trạm phát sóng B có bán kính hoạt động lần lượt là 50 km và (50sqrt 3 ) km. Tính diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B. Biết rằng nếu khoảng cách từ thiết bị thu sóng đến trạm phát sóng lớn hơn bán kính hoạt động của trạm phát sóng thì thiết bị không thu được sóng của trạm phát sóng đó.
Đề bài
Hai trạm phát sóng A và B đặt cách nhau 100 km. Trạm phát sóng A và trạm phát sóng B có bán kính hoạt động lần lượt là 50 km và \(50\sqrt 3 \) km. Tính diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B. Biết rằng nếu khoảng cách từ thiết bị thu sóng đến trạm phát sóng lớn hơn bán kính hoạt động của trạm phát sóng thì thiết bị không thu được sóng của trạm phát sóng đó.
Phương pháp giải - Xem chi tiết
Dựa vào: Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) được tính bởi công thức: \(S = \pi ({R^2} - {r^2})\).
Lời giải chi tiết
Gọi C và D là giao điểm của hai đường tròn (A; 50 km) và (B; \(50\sqrt 3 \) km).
Ta thấy AB2 = AC2 + BC2, suy ra tam giác ABC vuông tại C.
Tam giác ABC có sin B =\(\frac{{AC}}{{AB}} = \frac{1}{2}\),
suy ra \(\widehat B = {30^o}\);
suy ra \(\widehat A = {60^o}\),
suy ra \(\widehat {CBD} = {60^o},\) \(\widehat {CAD} = {120^o}\).
Do đó tam giác BCD đều, suy ra CD = \(50\sqrt 3 \) km.
Diện tích hình quạt tròn giới hạn bởi bán kính AC, bán kính AD và cung nhỏ CD của (A; 50 km) là:
\({S_1} = \frac{{\pi {{.50}^2}.120}}{{360}} = \frac{{2500\pi }}{3}(k{m^2})\).
Diện tích hình quạt tròn giới hạn bởi bán kính BD, bán kính BC và cung nhỏ CD của (A; \(50\sqrt 3 \) km) là:
\({S_2} = \frac{{\pi .{{\left( {50\sqrt 3 } \right)}^2}.60}}{{360}} = 1250\pi (k{m^2})\).
Diện tích tứ giác ABCD là:
\({S_{ABCD}} = \frac{1}{2}.AB.CD = \frac{1}{2}.100.50\sqrt 3 = 2500\sqrt 3 (k{m^2})\).
Diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B là:
\({S_1} + {S_2} - {S_{ABCD}} = \frac{{2500\pi }}{3} + 1250\pi - 2500\sqrt 3 \approx 2214,86(k{m^2}).\)
Bài 5 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như hệ số góc, giao điểm của đồ thị hàm số, và điều kiện để hàm số đồng biến hoặc nghịch biến.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải bài 5 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1, chúng ta cần thực hiện các bước sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 5 (giả sử bài 5 có 3 phần a, b, c):
Đề bài: (Ví dụ: Xác định hàm số y = ax + b biết đồ thị hàm số đi qua hai điểm A(1; 2) và B(-1; 0)).
Lời giải: Thay tọa độ của điểm A và B vào phương trình y = ax + b, ta được hệ phương trình:
a + b = 2
-a + b = 0
Giải hệ phương trình này, ta được a = 1 và b = 1. Vậy hàm số cần tìm là y = x + 1.
Đề bài: (Ví dụ: Tìm giao điểm của hai đường thẳng y = 2x - 1 và y = -x + 2).
Lời giải: Để tìm giao điểm, ta giải phương trình 2x - 1 = -x + 2. Từ đó suy ra 3x = 3, hay x = 1. Thay x = 1 vào một trong hai phương trình, ta được y = 1. Vậy giao điểm của hai đường thẳng là (1; 1).
Đề bài: (Ví dụ: Một ô tô đi từ A đến B với vận tốc 60km/h. Hỏi sau bao lâu ô tô đến B nếu quãng đường AB dài 180km?).
Lời giải: Thời gian ô tô đi từ A đến B là t = s/v = 180/60 = 3 giờ.
Để giải nhanh các bài tập về hàm số, bạn nên:
Để học toán 9 hiệu quả hơn, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 5 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!