Bài 7 trang 73 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7 trang 73 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
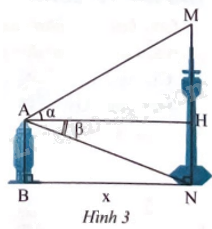
Khoảng cách giữa hai chân tháp AB và MN là x (Hình 3). So với phương nằm ngang AH, từ đỉnh A của tháp AB nhìn lên đỉnh M của tháp MN ta được góc (alpha ), từ đỉnh A của tháp AB nhìn xuống chân N của tháp MN ta được góc (beta ). Cho biết x = 120 m, (alpha ) = 30o và (beta ) = 20o . Chiều cao của tháp MN (kết quả làm tròn đến hàng đơn vị của mét) là A. 113 m B. 25 m C. 101 m D. 21,7 m
Đề bài
Khoảng cách giữa hai chân tháp AB và MN là x (Hình 3). So với phương nằm ngang AH, từ đỉnh A của tháp AB nhìn lên đỉnh M của tháp MN ta được góc \(\alpha \), từ đỉnh A của tháp AB nhìn xuống chân N của tháp MN ta được góc \(\beta \). Cho biết x = 120 m, \(\alpha \) = 30o và \(\beta \) = 20o . Chiều cao của tháp MN (kết quả làm tròn đến hàng đơn vị của mét) là
A. 113 m
B. 25 m
C. 101 m
D. 21,7 m
Phương pháp giải - Xem chi tiết
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
Ta có AH = BN = 120 m
tan \(\alpha = \frac{{MH}}{{AH}}\), suy ra MH = tan \(\alpha .AH = \tan {30^o}.120 = 40\sqrt 3 (m)\).
tan \(\beta = \frac{{NH}}{{AH}}\) suy ra NH = tan \(\beta .AH = \tan {20^o}.120 \approx 43,7(m)\).
Vậy MN = MH + NH \( \approx 40\sqrt 3 + 43,7 \approx 113\) m.
Chọn đáp án A.
Bài 7 trang 73 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 7 trang 73, yêu cầu thường là tìm hệ số góc của đường thẳng, xác định đường thẳng song song với một đường thẳng cho trước, hoặc giải các bài toán ứng dụng liên quan đến hàm số bậc nhất.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét từng phần của bài tập. Ví dụ, nếu bài tập yêu cầu tìm hệ số góc của đường thẳng có phương trình y = ax + b, thì hệ số góc chính là giá trị của a. Nếu bài tập yêu cầu xác định đường thẳng song song với đường thẳng y = a'x + b', thì đường thẳng cần tìm phải có cùng hệ số góc a' với đường thẳng đã cho.
Dưới đây là một ví dụ minh họa:
Ví dụ: Tìm hệ số góc của đường thẳng y = 2x - 3.
Giải: Hệ số góc của đường thẳng y = 2x - 3 là 2.
Bài 7 trang 73 thường xuất hiện các dạng bài tập sau:
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 hoặc các nguồn tài liệu học tập khác.
Bài 7 trang 73 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bằng cách nắm vững kiến thức cơ bản, phân tích đề bài một cách cẩn thận và vận dụng các phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài tập này một cách hiệu quả.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình hàm số bậc nhất, trong đó a là hệ số góc, b là tung độ gốc. |
| a = a' | Điều kiện để hai đường thẳng y = ax + b và y = a'x + b' song song. |