Giải bài 2 trang 92 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1

Giải bài 2 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Giải bài 2 trang 92 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1

Bài 2 trang 92 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 92 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho đường tròn (O; R) và dây cung MN = (Rsqrt 3 ). Tính số đo của mỗi cung (oversetfrown{MN}) (cung lớn và cung nhỏ).

Đề bài

Cho đường tròn (O; R) và dây cung MN = \(R\sqrt 3 \). Tính số đo của mỗi cung \(\overset\frown{MN}\) (cung lớn và cung nhỏ).

Phương pháp giải - Xem chi tiết Giải bài 2 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1 1

Dựa vào: Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. Số đo của cung lớn bằng hiệu giữa 360^o và số đo cung nhỏ có chung hai đầu mút với cung lớn.

Lời giải chi tiết

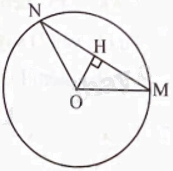
Giải bài 2 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1 2

Kẻ \(OH \bot MN\)tại H. Ta có OM = ON = R, suy ra tam giác OMN cân tại O, suy ra HM = HN.

Dó đó HM = HN = \(\frac{{MN}}{2} = \frac{{R\sqrt 3 }}{2}\).

Ta có: \(cos\widehat {HMO} = \frac{{HM}}{2} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2},\)

Nên \(\widehat {HMO} = {30^o}\), suy ra \(\widehat {MON} = {120^o}\).

Suy ra số đo cung nhỏ \(\overset\frown{MN}\) là 120^o, số đo cung lớn \(\overset\frown{MN}\) = 360^o – 120^o = 240^o.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 2 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1 đặc sắc thuộc chuyên mục toán 9 sgk trên nền tảng môn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 2 trang 92 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1: Chi tiết và Dễ hiểu

Bài 2 trang 92 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc xác định các yếu tố của hàm số bậc nhất và ứng dụng vào việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết, từng bước, giúp học sinh hiểu rõ phương pháp và tự tin giải bài tập.

Nội dung bài tập:

Bài 2 yêu cầu học sinh xác định hệ số góc của đường thẳng và kiểm tra xem hai đường thẳng có song song hay không. Để giải bài tập này, học sinh cần nắm vững các khái niệm sau:

Hàm số bậc nhất: Hàm số có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
Hệ số góc: Hệ số a trong hàm số y = ax + b. Hệ số góc quyết định độ dốc của đường thẳng.
Đường thẳng song song: Hai đường thẳng song song khi và chỉ khi chúng có cùng hệ số góc và khác tung độ gốc.

Lời giải chi tiết:

Để giải bài 2 trang 92, chúng ta cần phân tích từng phần của bài tập và áp dụng các kiến thức đã học. Giả sử bài tập đưa ra hai hàm số:

y = 2x + 3 và y = 2x - 1

Xác định hệ số góc của mỗi hàm số:

Hàm số y = 2x + 3 có hệ số góc a = 2.
Hàm số y = 2x - 1 có hệ số góc a = 2.

Kiểm tra xem hai đường thẳng có song song hay không:

Vì hai hàm số có cùng hệ số góc a = 2 nhưng khác tung độ gốc (3 ≠ -1), nên hai đường thẳng tương ứng là song song.

Các dạng bài tập tương tự:

Ngoài bài 2, chương Hàm số bậc nhất còn có nhiều bài tập tương tự. Các bài tập này thường yêu cầu học sinh:

Xác định hệ số góc và tung độ gốc của hàm số.
Viết phương trình đường thẳng khi biết hệ số góc và một điểm thuộc đường thẳng.
Kiểm tra xem một điểm có thuộc đường thẳng hay không.
Tìm giao điểm của hai đường thẳng.

Mẹo giải bài tập Hàm số bậc nhất:

Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, học sinh nên:

Nắm vững các khái niệm cơ bản về hàm số bậc nhất, hệ số góc và đường thẳng song song.
Luyện tập giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra kết quả.

Ứng dụng của Hàm số bậc nhất trong thực tế:

Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:

Tính quãng đường đi được của một vật chuyển động đều.
Dự đoán doanh thu của một công ty.
Mô tả sự thay đổi nhiệt độ theo thời gian.

Kết luận:

Bài 2 trang 92 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn trong việc học Toán 9.

Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức Toán học. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải Toán 9 khác và các tài liệu học tập hữu ích.