Bài 4 trang 99 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 99, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài tập.
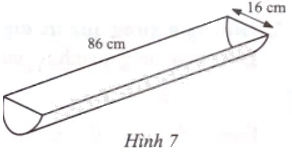
Phần bên trong của một máng nước có dạng nửa hình trụ với đường kính đáy 16 cm, chiều cao 86 cm (Hình 7). Tính dung tích của máng nước (kết quả làm tròn đến hàng đơn vị của lít).
Đề bài
Phần bên trong của một máng nước có dạng nửa hình trụ với đường kính đáy 16 cm, chiều cao 86 cm (Hình 7). Tính dung tích của máng nước (kết quả làm tròn đến hàng đơn vị của lít).
Phương pháp giải - Xem chi tiết
Thể tích hình trụ: \(V = \pi {r^2}h\).
Lời giải chi tiết
Dung tích của máng nước bằng nửa thể tích của hình trụ có cùng bán kính đáy và chiều cao:
V = \(\frac{{\pi {r^2}h}}{2} = \frac{{\pi {{.8}^2}.86}}{2} = 2752\pi \) (cm3) \( \approx 9(l)\).
Bài 4 yêu cầu chúng ta xét một hàm số bậc hai và xác định các yếu tố của nó, bao gồm hệ số a, b, c, đỉnh của parabol, trục đối xứng và khoảng giá trị của hàm số. Bài toán này giúp củng cố kiến thức về dạng tổng quát của hàm số bậc hai và cách xác định các đặc điểm quan trọng của nó.
Để giải bài 4 trang 99 sách bài tập Toán 9 - Chân trời sáng tạo tập 2, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cho trong bài là y = 2x2 - 8x + 5. Ta thực hiện như sau:
Ngoài việc giải bài 4 trang 99, các em học sinh cũng nên luyện tập thêm các bài tập tương tự để nắm vững kiến thức về hàm số bậc hai. Các em có thể tham khảo thêm các tài liệu sau:
Khi giải bài tập về hàm số bậc hai, các em cần chú ý những điều sau:
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 4 trang 99 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi giải bài tập này và các bài tập tương tự.