Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 3 trang 7 trong sách bài tập Toán 9 - Chân trời sáng tạo tập 2.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho parabol (P): y = (frac{3}{2})x2 và đường thẳng d: y = 3x. a) Vẽ (P) và d trên cùng một mặt phẳng toạ độ Oxy. b) Dựa vào hình vẽ, tìm toạ độ giao điểm của (P) và d.
Đề bài
Cho parabol (P): y = \(\frac{3}{2}\)x2 và đường thẳng d: y = 3x.
a) Vẽ (P) và d trên cùng một mặt phẳng toạ độ Oxy.
b) Dựa vào hình vẽ, tìm toạ độ giao điểm của (P) và d.
Phương pháp giải - Xem chi tiết
Lập bảng giá trị của hàm số.
Vẽ đồ thị hàm số.
Nhìn đồ thị để kết luận.
Lời giải chi tiết
a) Đồ thị hàm số y = \(\frac{3}{2}\)x2 là một đường parabol đỉnh O đi qua các điểm A(-2;6), \(B\left( { - 1;\frac{3}{2}} \right)\), O(0;0), \(B'\left( {1;\frac{3}{2}} \right)\), A’(2;6).
Đồ thị hàm số y = 3x là đường thẳng đi qua các điểm O(0;0) và A’(2;6).
Đồ thị của hai hàm số y = \(\frac{3}{2}\)x2 và y = 3x được vẽ như hình dưới.
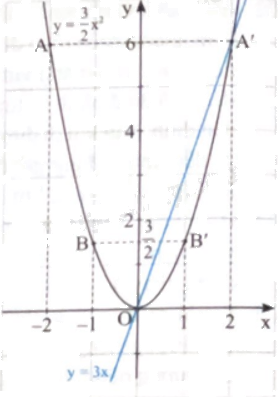
b) Dựa vào hình vẽ, ta có các giao điểm của (P) và d là O(0;0) và A’(2;6).
Bài 3 trang 7 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về xác định hàm số, tính giá trị của hàm số tại một điểm cho trước, và tìm điều kiện để hàm số đồng biến hoặc nghịch biến. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 3 trang 7, chúng tôi sẽ trình bày lời giải chi tiết cho từng dạng bài tập:
Cho hàm số y = (m - 2)x + 3. Tìm giá trị của m để hàm số là hàm số bậc nhất.
Lời giải:
Để hàm số y = (m - 2)x + 3 là hàm số bậc nhất, thì hệ số a phải khác 0. Do đó, ta có:
m - 2 ≠ 0
m ≠ 2
Vậy, với m ≠ 2, hàm số y = (m - 2)x + 3 là hàm số bậc nhất.
Cho hàm số y = 2x - 1. Tính giá trị của y khi x = 3.
Lời giải:
Thay x = 3 vào hàm số y = 2x - 1, ta được:
y = 2 * 3 - 1 = 6 - 1 = 5
Vậy, khi x = 3, thì y = 5.
Cho hàm số y = (k + 1)x + 2. Tìm giá trị của k để hàm số đồng biến.
Lời giải:
Để hàm số y = (k + 1)x + 2 đồng biến, thì hệ số a phải lớn hơn 0. Do đó, ta có:
k + 1 > 0
k > -1
Vậy, với k > -1, hàm số y = (k + 1)x + 2 đồng biến.
Bài 3 trang 7 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán.