Bài 6 trang 107 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 107, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
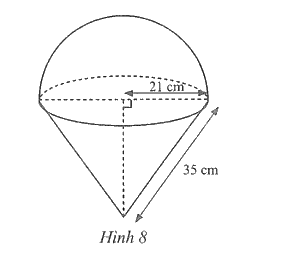
Một vật thể đặc gồm một phần dạng nửa hình cầu và một phần dạng hình nón với các số đo như Hình 8. Tính thể tích và diện tích bề mặt của vật thể này (kết quả làm tròn đến hàng đơn vị của xăngtimét khối, xăngtimét vuông).
Đề bài
Một vật thể đặc gồm một phần dạng nửa hình cầu và một phần dạng hình nón với các số đo như Hình 8. Tính thể tích và diện tích bề mặt của vật thể này (kết quả làm tròn đến hàng đơn vị của xăngtimét khối, xăngtimét vuông).
Phương pháp giải - Xem chi tiết
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\).
Thể tích của hình nón: \(V = \frac{1}{3}\pi {r^2}h\).
Diện tích mặt cầu là: \(S = 4\pi {R^2}\).
Thể tích hình cầu là: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết
Chiều cao của hình nón là:
h = \(\sqrt {{{35}^2} - {{21}^2}} = 28\) (cm).
Thể tích của hình nón là:
\({V_1} = \frac{1}{3}\pi {.21^2}.28 = 4116\pi \) (cm3).
Thể tích của nửa hình cầu là:
\({V_2} = \frac{1}{2}.\frac{4}{3}.\pi {.21^3} = 6174\pi \) (cm3).
Thể tích của vật thể là:
\(V = {V_1} + {V_2} = 4116\pi + 6174\pi = 10290\pi \approx 32327\) (cm3).
Diện tích xung quanh của hình nón là:
\({S_1} = \pi .21.35 = 735\pi \) (cm2).
Diện tích bề mặt của nửa hình cầu là:
\({S_2} = \frac{1}{2}.4.\pi {.21^2} = 882\pi \) (cm2).
Diện tích bề mặt của vật thể là:
\(S = {S_1} + {S_2} = 735\pi + 882\pi = 1617\pi \approx 5080\) (cm2).
Bài 6 trang 107 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập 6 yêu cầu học sinh xác định hệ số góc và tung độ gốc của đường thẳng đi qua hai điểm cho trước. Sau đó, học sinh cần viết phương trình đường thẳng đó.
Để giải bài tập này, học sinh có thể sử dụng các phương pháp sau:
Bài 6: Xác định hệ số góc và tung độ gốc của đường thẳng đi qua hai điểm A(1; 3) và B(-2; 0).
Giải:
Hệ số góc của đường thẳng AB là: m = (0 - 3) / (-2 - 1) = (-3) / (-3) = 1.
Phương trình đường thẳng AB có dạng: y = mx + b.
Thay tọa độ điểm A(1; 3) vào phương trình, ta được: 3 = 1 * 1 + b => b = 2.
Vậy, hệ số góc của đường thẳng AB là 1 và tung độ gốc là 2.
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý:
Bài 6 trang 107 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.