Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 8 trang 49 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 8 trang 49 một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
Vào đầu năm học, người ta lựa chọn ngẫu nhiên một số học sinh lớp 9 ở khu vực A và khu vực B để kiểm tra tình trạng cân nặng. Kết quả khảo sát được ghi lại ở bảng sau: a) Hãy tính tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng. b) Hãy lựa chọn, vẽ biểu đồ phù hợp và so sánh tình trạng cân nặng của học sinh ở hai khu vực.
Đề bài
Vào đầu năm học, người ta lựa chọn ngẫu nhiên một số học sinh lớp 9 ở khu vực A và khu vực B để kiểm tra tình trạng cân nặng. Kết quả khảo sát được ghi lại ở bảng sau:
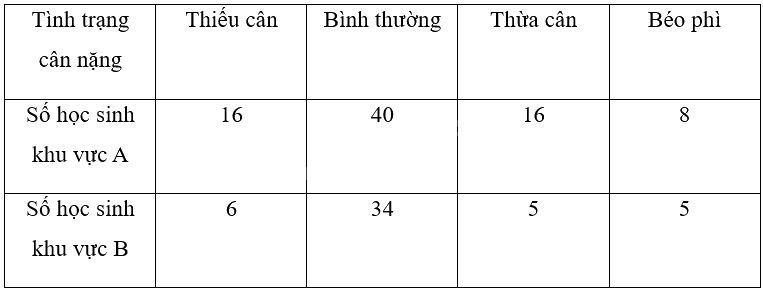
a) Hãy tính tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng.
b) Hãy lựa chọn, vẽ biểu đồ phù hợp và so sánh tình trạng cân nặng của học sinh ở hai khu vực.
Phương pháp giải - Xem chi tiết
Dựa vào: Công thức tần số tương đối của mỗi nhóm là \(f = \frac{m}{N}.100\% \) (m là tần số nhóm, N là cỡ mẫu).
Bảng tần số tương đối ghép nhóm có dạng:

Sử dụng biểu đồ tần số dạng cột kép để dễ dàng so sánh tần số tương đối của các giá trị thuộc hai nhóm đối tượng khác nhau.
Nhìn vào biểu đồ và nhận xét.
Lời giải chi tiết
a) Bảng tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng:
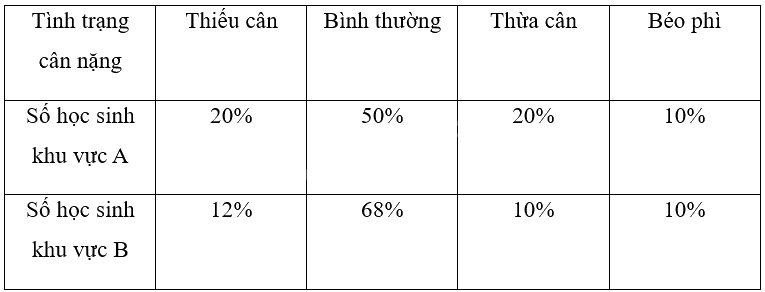
b) Để so sánh tình trạng cân nặng của học sinh ở hai khu vực, ta sử dụng biểu đồ tần số tương đối dạng cột kép.
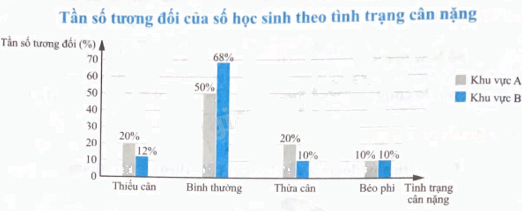
Tần số tương đối của học sinh thiếu cân và thừa cân ở khu vực A cao hơn khu vực B.
Tần số tương đối của học sinh bình thường ở khu vực A thấp hơn khu vực B.
Tần số tương đối của học sinh béo phì ở hai khu vực là như nhau.
Bài 8 trang 49 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài 8 bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 8 trang 49, chúng tôi sẽ trình bày lời giải chi tiết cho từng dạng bài tập.
Ví dụ 1: Xác định hàm số bậc nhất có đồ thị là đường thẳng đi qua hai điểm A(1; 2) và B(-1; 0).
Lời giải:
Ví dụ 2: Cho hàm số y = 2x - 3. Tính giá trị của y khi x = -2.
Lời giải:
Thay x = -2 vào hàm số y = 2x - 3, ta được:
y = 2(-2) - 3 = -4 - 3 = -7
Vậy, khi x = -2 thì y = -7.
Ví dụ 3: Một người đi xe máy với vận tốc 40 km/h. Gọi x là thời gian đi (tính bằng giờ) và y là quãng đường đi được (tính bằng km). Hãy viết công thức tính quãng đường đi được theo thời gian.
Lời giải:
Quãng đường đi được bằng vận tốc nhân với thời gian. Do đó, công thức tính quãng đường đi được theo thời gian là:
y = 40x
Bài 8 trang 49 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!