Bài 15 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 15 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
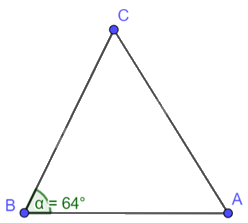
Cho tam giác ABC có AB = 15 cm, BC = 20 cm, (widehat {ABC} = {64^o}). Tính độ dài: a) đường cao AH; b) các đoạn thẳng BH, CH; c) cạnh AC
Đề bài
Cho tam giác ABC có AB = 15 cm, BC = 20 cm, \(\widehat {ABC} = {64^o}\). Tính độ dài:
a) đường cao AH;
b) các đoạn thẳng BH, CH;
c) cạnh AC
Phương pháp giải - Xem chi tiết
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
a) AH = AB. sin \(\widehat {ABC}\) = \(15.\sin {64^o} \approx 13,48(cm)\)
b) BH = AB. \(\cos \widehat {ABC} = 15.\cos {64^o} \approx 6,58(cm)\);
CH = BC – BH \( \approx 20 - 6,58 = 13,42(cm)\);
c) \(AC = \sqrt {A{H^2} + C{H^2}} \approx \sqrt {{{13,48}^2} + {{13,42}^2}} \approx 19,02(cm).\)
Bài 15 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc, đường thẳng song song, vuông góc và ứng dụng vào giải quyết các bài toán liên quan đến thực tế.
Bài 15 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 15 trang 75, chúng ta sẽ đi vào phân tích từng phần của bài tập.
(Giả sử câu a yêu cầu xác định hệ số góc của đường thẳng y = 2x - 3)
Hệ số góc của đường thẳng y = 2x - 3 là 2. Điều này được xác định dựa trên dạng tổng quát của hàm số bậc nhất y = ax + b, trong đó 'a' là hệ số góc.
(Giả sử câu b yêu cầu tìm phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc là -1)
Phương trình đường thẳng có dạng y = ax + b. Thay a = -1 và tọa độ điểm A(1; 2) vào phương trình, ta có:
2 = -1 * 1 + b
=> b = 3
Vậy phương trình đường thẳng cần tìm là y = -x + 3.
(Giả sử câu c yêu cầu xác định xem hai đường thẳng y = 3x + 1 và y = -3x + 2 có song song hay không)
Hai đường thẳng song song khi và chỉ khi chúng có cùng hệ số góc. Trong trường hợp này, hệ số góc của đường thẳng y = 3x + 1 là 3, và hệ số góc của đường thẳng y = -3x + 2 là -3. Vì hai hệ số góc khác nhau, nên hai đường thẳng này không song song.
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Bài 15 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
Để luyện tập thêm, các em có thể tham khảo các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 hoặc trên các trang web học toán online khác.