Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Bài 8 trang 98 sách bài tập toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số, đồ thị hàm số và các tính chất của hàm số để tìm ra lời giải chính xác.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 98 sách bài tập toán 9 Chân trời sáng tạo tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

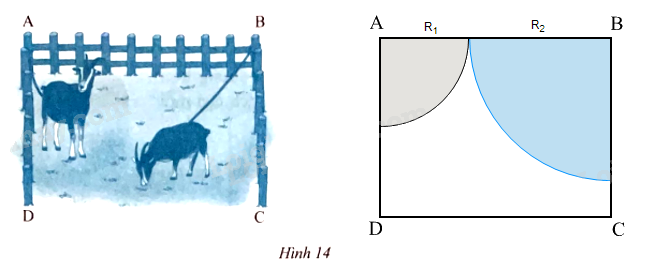
Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc: Cách 1: Mỗi dây thừng dài 20 m. Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m. Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn?

Đề bài

Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc:

Cách 1: Mỗi dây thừng dài 20 m.

Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m.

Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn?

Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 1

Phương pháp giải - Xem chi tiết Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 2

Dựa vào: Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).

Lời giải chi tiết

Diện tích cỏ hai con dê có thể ăn là dạng hai hình quạt có số đo cung cùng bằng 90^o.

TH1: Mỗi dây thừng dài 20 m suy ra R₁ = R₂ = 20 m.

Diện tích cỏ mà hai con dê có thể ăn:

\(S = {S_1} + {S_2} = \frac{{\pi R_1^2.90}}{{360}} + \frac{{\pi R_2^2.90}}{{360}} \\= \frac{{\pi {{.20}^2}.90}}{{360}} + \frac{{\pi {{.20}^2}.90}}{{360}} = 200\pi ({m^2})\)

TH2: Giả sử dây thừng cột con dê ở A dài 30 m, dây thừng cột con dê ở B dài 10 m.

Suy ra R₁ = 30 m, R₂ = 10 m.

Diện tích cỏ mà hai con dê có thể ăn:

\(S = {S_1} + {S_2} = \frac{{\pi R_1^2.90}}{{360}} + \frac{{\pi R_2^2.90}}{{360}} \\= \frac{{\pi {{.30}^2}.90}}{{360}} + \frac{{\pi {{.10}^2}.90}}{{360}} = 250\pi ({m^2}).\)

Vậy dùng hai sợi dây 30 m và 10 m thì diện tích cỏ hai con dê sẽ ăn nhiều hơn.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 đặc sắc thuộc chuyên mục giải toán 9 trên nền tảng toán math. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải

Bài 8 trang 98 sách bài tập toán 9 Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài tập này thường xoay quanh việc xác định hàm số, vẽ đồ thị hàm số, và ứng dụng hàm số vào giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:

Hàm số bậc nhất: Định nghĩa, dạng tổng quát y = ax + b (a ≠ 0).
Hệ số a và b: Ý nghĩa của hệ số a (độ dốc) và b (giao điểm với trục Oy).
Đồ thị hàm số: Cách vẽ đồ thị hàm số bậc nhất, xác định các điểm thuộc đồ thị.
Tính chất của hàm số: Hàm số đồng biến, nghịch biến.

Lời giải chi tiết bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài tập. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận giải một bài tập tương tự:

Ví dụ:

Cho hàm số y = 2x - 3. Hãy:

Vẽ đồ thị hàm số.
Tìm tọa độ giao điểm của đồ thị hàm số với trục Ox và trục Oy.
Xác định xem hàm số đồng biến hay nghịch biến.

Giải:

Vẽ đồ thị hàm số:
Để vẽ đồ thị hàm số y = 2x - 3, ta cần xác định hai điểm thuộc đồ thị. Ví dụ, ta chọn x = 0 thì y = -3, và chọn x = 1 thì y = -1. Vẽ đường thẳng đi qua hai điểm (0, -3) và (1, -1).
Tìm tọa độ giao điểm:
- Giao điểm với trục Oy: Khi x = 0, y = -3. Vậy tọa độ giao điểm là (0, -3).
- Giao điểm với trục Ox: Khi y = 0, 2x - 3 = 0 => x = 3/2. Vậy tọa độ giao điểm là (3/2, 0).
Xác định tính chất của hàm số:
Vì hệ số a = 2 > 0, nên hàm số y = 2x - 3 là hàm số đồng biến.

Các dạng bài tập thường gặp và phương pháp giải

Ngoài dạng bài tập vẽ đồ thị và tìm giao điểm, bài 8 trang 98 sách bài tập toán 9 Chân trời sáng tạo tập 1 còn có thể xuất hiện các dạng bài tập sau:

Xác định hàm số khi biết đồ thị: Dựa vào đồ thị để tìm hệ số a và b của hàm số y = ax + b.
Ứng dụng hàm số vào giải quyết bài toán thực tế: Ví dụ, bài toán về quãng đường, thời gian, vận tốc.
Tìm điều kiện để hàm số thỏa mãn một điều kiện nào đó: Ví dụ, tìm m để hàm số y = (m-1)x + 2 đồng biến.

Để giải quyết các dạng bài tập này, học sinh cần:

Nắm vững các kiến thức cơ bản về hàm số bậc nhất.
Rèn luyện kỹ năng vẽ đồ thị hàm số.
Luyện tập giải nhiều bài tập khác nhau để làm quen với các dạng bài tập và phương pháp giải.

Lưu ý khi giải bài tập

Khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý:

Đọc kỹ đề bài để hiểu rõ yêu cầu của bài tập.
Sử dụng các công thức và định lý một cách chính xác.
Kiểm tra lại kết quả sau khi giải xong.

Tổng kết

Bài 8 trang 98 sách bài tập toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Bằng cách nắm vững các kiến thức cơ bản, rèn luyện kỹ năng giải bài tập, và lưu ý các điểm quan trọng, học sinh có thể tự tin giải quyết bài tập này một cách hiệu quả.