Bài 16 trang 101 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 16 trang 101, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
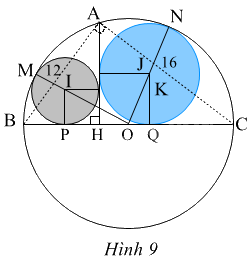
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O). Tính: a) BC, BH. b) Bán kính R, R’ của đường tròn (I) và (J). c) Khoảng cách PQ.
Đề bài
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O). Tính:
a) BC, BH.
b) Bán kính R, R’ của đường tròn (I) và (J).
c) Khoảng cách PQ.
Phương pháp giải - Xem chi tiết
Dựa vào: định lý Pytago để chứng minh.
Lời giải chi tiết
a) \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{12}^2} + {{16}^2}} = 20\).
\(\Delta BHA\backsim \Delta BAC\) suy ra BA2 = BH.BC, suy ra BH = \(\frac{{B{A^2}}}{{BC}} = \frac{{36}}{5}.\)
b) \(OH = OB – BH = 10 - \frac{{36}}{5} = \frac{{14}}{5}.\)
Áp dụng định lí Pytago trong tam giác IPO vuông tại P, ta có
IO2 = IP2 + PO2, suy ra (10 – R)2 = R2 + \({\left( {R + \frac{{14}}{5}} \right)^2}\), suy ra R = \(\frac{{16}}{5}\).
Áp dụng định lí Pytago trong tam giác JQO vuông tại Q, ta có
JO2 = JQ2 + QO2 ,
suy ra (10 – R’)2 = R’2 + \({\left( {R' - \frac{{14}}{5}} \right)^2}\),
suy ra \(R’ = \frac{{24}}{5}\).
c) Ta có PQ = PH + QH = R + R’ = 8.
Bài 16 trang 101 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc xác định hệ số góc và đường thẳng song song, vuông góc. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng để giải quyết bài toán này.
Bài 16 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 16 trang 101 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Câu a: Cho đường thẳng y = 2x - 3. Xác định hệ số góc của đường thẳng này.
Giải: Hệ số góc của đường thẳng y = 2x - 3 là a = 2.
Câu b: Tìm m để đường thẳng y = (m - 1)x + 2 song song với đường thẳng y = 3x + 1.
Giải: Để hai đường thẳng song song, ta cần có m - 1 = 3 và 2 ≠ 1. Suy ra m = 4.
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 hoặc trên các trang web học toán online.
Bài 16 trang 101 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp các em học sinh hiểu sâu hơn về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên đây, các em sẽ tự tin hơn khi làm bài tập Toán 9.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hệ số góc | a trong y = ax + b |
| Đường thẳng song song | a1 = a2, b1 ≠ b2 |
| Đường thẳng vuông góc | a1 * a2 = -1 |