Bài 1 trang 98 sách bài tập Toán 9 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số, tìm đỉnh của parabol và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1 trang 98, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình trụ có chiều cao 10 cm, đường kính đáy 7 cm (Hình 5a) và hình khai triển của hình trụ đó (Hình 5b). Hãy viết số thích hợp vào mỗi dấu ? trong hình vẽ.
Đề bài
Cho hình trụ có chiều cao 10 cm, đường kính đáy 7 cm (Hình 5a) và hình khai triển của hình trụ đó (Hình 5b). Hãy viết số thích hợp vào mỗi dấu ? trong hình vẽ.
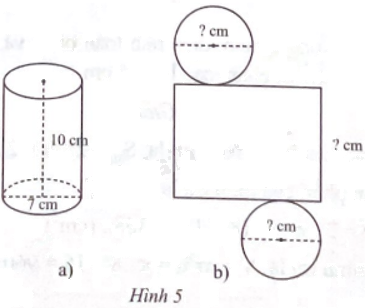
Phương pháp giải - Xem chi tiết
Nhìn vào hình bên trái để điền số thích hợp.
Lời giải chi tiết
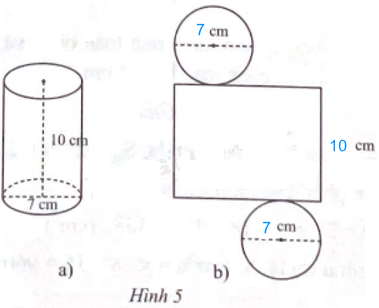
Bài 1 trang 98 sách bài tập Toán 9 Chân trời sáng tạo tập 2 yêu cầu học sinh xét hàm số y = x2 - 4x + 3. Bài tập này bao gồm các phần nhỏ sau:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c. So sánh hai vế, ta dễ dàng xác định được:
Sử dụng công thức tính tọa độ đỉnh, ta có:
Vậy tọa độ đỉnh của parabol là (2, -1).
Trục đối xứng của parabol là đường thẳng x = xđỉnh = 2.
Vì a = 1 > 0, parabol có dạng mở lên trên. Do đó:
Để vẽ đồ thị hàm số, ta cần tìm thêm một vài điểm:
Dựa vào các điểm đã tìm được, ta có thể vẽ được đồ thị hàm số y = x2 - 4x + 3.
Khi giải bài tập về hàm số bậc hai, học sinh cần nắm vững các công thức tính tọa độ đỉnh, trục đối xứng và khoảng đồng biến, nghịch biến. Ngoài ra, việc vẽ đồ thị hàm số cũng rất quan trọng để hiểu rõ tính chất của hàm số.
Để rèn luyện thêm kỹ năng giải bài tập về hàm số bậc hai, học sinh có thể tham khảo các bài tập tương tự trong sách bài tập Toán 9 Chân trời sáng tạo tập 2.