Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 10 sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin hơn khi giải các bài tập tương tự.
Biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng toạ độ Oxy. a) 2x + y = - 2 b) 0x – y = -3 c) – 4x + 0y = 6
Đề bài
Biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng toạ độ Oxy.
a) 2x + y = - 2
b) 0x – y = -3
c) – 4x + 0y = 6
Phương pháp giải - Xem chi tiết
Viết lại các phương trình thành y = ax + b.
Lấy 2 điểm thuộc đường thẳng
Vẽ trên mặt phẳng toạ độ Oxy và kết luận.
Lời giải chi tiết
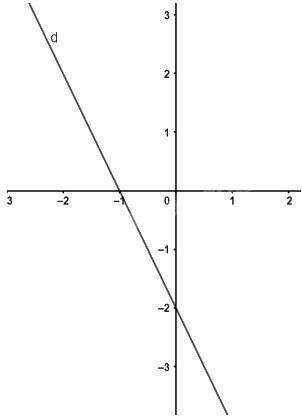
a) Viết lại phương trình thành y = - 2x – 2.
Tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = -2x – 2.
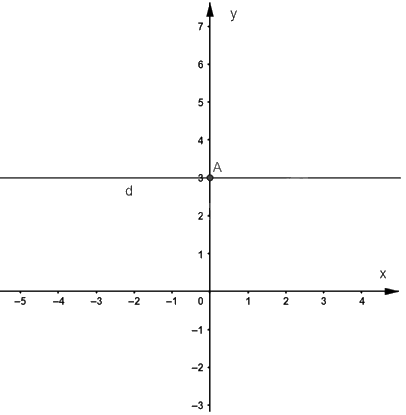
b) Viết lại phương trình thành y = 3.
Tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với trục Oy tại A(0;3).
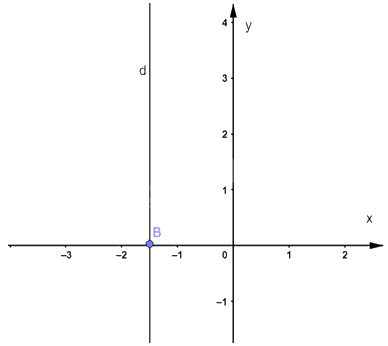
c) Viết lại phương trình thành \(x = - \frac{3}{2}\).
Tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với trục Ox tại B \(\left( { - \frac{3}{2};0} \right)\).
Bài 3 trang 10 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và đường thẳng song song, vuông góc.
Bài 3 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 3 trang 10 sách bài tập Toán 9 - Chân trời sáng tạo tập 1:
Đường thẳng có dạng y = ax + b. Hệ số góc của đường thẳng là a. Để xác định a, ta cần biết tọa độ của hai điểm thuộc đường thẳng hoặc một điểm và góc nghiêng của đường thẳng.
Ví dụ: Nếu đường thẳng đi qua điểm (x1, y1) và (x2, y2) thì a = (y2 - y1) / (x2 - x1).
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song khi và chỉ khi a1 = a2 và b1 ≠ b2.
Điều này có nghĩa là hai đường thẳng có cùng hệ số góc nhưng khác tung độ gốc.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 vuông góc khi và chỉ khi a1 * a2 = -1.
Điều này có nghĩa là tích của hệ số góc của hai đường thẳng bằng -1.
Để viết phương trình đường thẳng thỏa mãn các điều kiện cho trước, ta cần xác định hệ số góc và tung độ gốc. Sử dụng các thông tin về điểm mà đường thẳng đi qua, hệ số góc hoặc điều kiện song song, vuông góc với một đường thẳng khác để tìm ra các giá trị cần thiết.
Giả sử chúng ta có đường thẳng y = 2x - 1. Để viết phương trình đường thẳng song song với đường thẳng này và đi qua điểm (1, 3), ta làm như sau:
Khi giải bài tập về hàm số bậc nhất, cần chú ý đến các trường hợp đặc biệt như đường thẳng song song với trục Ox (a = 0) hoặc đường thẳng song song với trục Oy (x = hằng số).
Bài 3 trang 10 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!