Bài 16 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 16 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
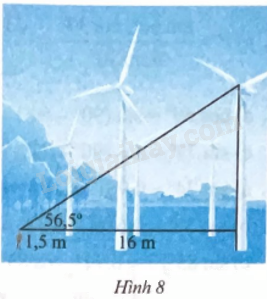
Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5o . Tính khoảng cách từ tâm của cánh quạt đến mặt đất, biết khoảng cách từ mắt của người đó đến mặt đất là 1,5 m.
Đề bài
Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5o . Tính khoảng cách từ tâm của cánh quạt đến mặt đất, biết khoảng cách từ mắt của người đó đến mặt đất là 1,5 m.
Phương pháp giải - Xem chi tiết
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
Gọi khoảng cách từ tâm của cánh quạt gió đến mặt đất là AE.
Người đứng ở vị trí điểm D, khoảng cách từ mắt người đó đến mặt đất là CD,
suy ra CD = BE = 1,5 m.
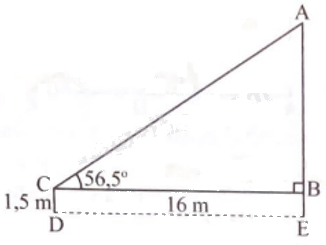
Người đứng cách thân quạt gió 16 m, suy ra DE = BC = 16 m.
Xét \(\Delta ABC\) vuông tại B có:
AB = BC. tan C = 16. tan 56,6o \( \approx 24,17(m)\).
AE = AB + BE \( \approx 24,17 + 1,5 \approx 25,67(m)\).
Vậy khoảng cách từ tâm quạt gió đến mặt đất là khoảng 25,67 m.
Bài 16 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản như:
Bài 16 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh giải bài 16 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 một cách hiệu quả, Giaitoan.edu.vn xin trình bày lời giải chi tiết cho từng dạng bài tập:
Để xác định hàm số, các em cần phân tích các thông tin cho trước và tìm mối liên hệ giữa các biến. Ví dụ, nếu đề bài cho biết hàm số đi qua hai điểm A(x1, y1) và B(x2, y2), các em có thể thay tọa độ của hai điểm này vào phương trình hàm số để tìm các hệ số.
Để tìm hệ số a, b, c của hàm số bậc hai, các em có thể sử dụng các phương pháp sau:
Để tính giá trị của hàm số tại một điểm cho trước, các em chỉ cần thay giá trị của biến vào phương trình hàm số và tính toán.
Để giải phương trình hoặc bất phương trình chứa hàm số, các em cần sử dụng các phương pháp đại số và các kiến thức về hàm số để tìm nghiệm.
Để vẽ đồ thị hàm số, các em cần xác định các yếu tố của đồ thị (đỉnh, trục đối xứng, giao điểm với các trục tọa độ) và vẽ các điểm trên đồ thị. Sau đó, các em nối các điểm này lại với nhau để được đồ thị hàm số.
Ví dụ 1: Xác định hàm số bậc nhất y = ax + b biết rằng hàm số đi qua hai điểm A(1, 2) và B(2, 4).
Giải: Thay tọa độ của điểm A vào phương trình hàm số, ta được: 2 = a(1) + b.
Thay tọa độ của điểm B vào phương trình hàm số, ta được: 4 = a(2) + b.
Giải hệ phương trình:
2 = a + b
4 = 2a + b
Ta được a = 2 và b = 0. Vậy hàm số cần tìm là y = 2x.
Ví dụ 2: Tìm hệ số a của hàm số bậc hai y = ax2 + bx + c biết rằng hàm số có đỉnh là I(1, -2).
Giải: Hoành độ đỉnh của parabol là x = -b/2a. Vì đỉnh I có hoành độ là 1, ta có: -b/2a = 1 => b = -2a.
Thay tọa độ của đỉnh I vào phương trình hàm số, ta được: -2 = a(1)2 + b(1) + c.
Thay b = -2a vào phương trình trên, ta được: -2 = a - 2a + c => c = a - 2.
Vậy hàm số có dạng y = ax2 - 2ax + a - 2.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 16 trang 75 Sách bài tập Toán 9 - Chân trời sáng tạo tập 1 một cách hiệu quả. Chúc các em học tốt!