Giải bài 4 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2

Giải bài 4 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2

Giải bài 4 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2

Bài 4 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Cho nửa đường tròn (O; R) có BC là đường kính. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF, Bx của nửa đường tròn (O) (F là tiếp điểm), tia AF cắt tia Bx tại D. Chứng minh OBDF là tứ giác nội tiếp.

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 4 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2 1

Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.

Lời giải chi tiết

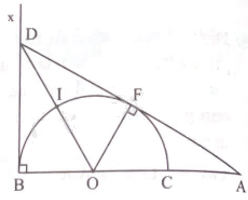
Giải bài 4 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2 2

Ta có \(\widehat {DBO} = {90^o}\) và \(\widehat {DFO} = {90^o}\)(tính chất của tiếp tuyến).

Gọi I trung điểm của DO.

Tam giác DBO vuông tại O nên nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO\).

Tương tự, tam giác DFO vuông tại F nên nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO\).

Do đó, tứ giác OBDF nội tiếp đường tròn tâm I, bán kính bằng \(\frac{1}{2}DO\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 4 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2 đặc sắc thuộc chuyên mục giải bài tập toán lớp 9 trên nền tảng môn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 4 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 4 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:

Hàm số bậc nhất: Định nghĩa, dạng tổng quát y = ax + b (a ≠ 0).
Hệ số a: Xác định tính chất đồng biến, nghịch biến của hàm số.
Hệ số b: Xác định giao điểm của đồ thị hàm số với trục tung.
Đồ thị hàm số bậc nhất: Cách vẽ đồ thị hàm số, xác định các điểm thuộc đồ thị.
Ứng dụng của hàm số bậc nhất: Giải các bài toán thực tế liên quan đến hàm số.

Lời giải chi tiết bài 4 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2

Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = 2x - 3. Tìm các điểm thuộc đồ thị hàm số có hoành độ là -1, 0, 1.)

Lời giải:

Với x = -1: Thay x = -1 vào hàm số y = 2x - 3, ta được y = 2*(-1) - 3 = -5. Vậy điểm cần tìm là A(-1; -5).
Với x = 0: Thay x = 0 vào hàm số y = 2x - 3, ta được y = 2*0 - 3 = -3. Vậy điểm cần tìm là B(0; -3).
Với x = 1: Thay x = 1 vào hàm số y = 2x - 3, ta được y = 2*1 - 3 = -1. Vậy điểm cần tìm là C(1; -1).

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài 4 trang 82, sách bài tập Toán 9 - Chân trời sáng tạo tập 2 còn nhiều bài tập tương tự. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:

Xác định hệ số a, b của hàm số: Sử dụng các điểm thuộc đồ thị hàm số để lập hệ phương trình và giải tìm a, b.
Vẽ đồ thị hàm số: Chọn các điểm thuộc đồ thị hàm số (ví dụ: giao điểm với trục tung, trục hoành) và vẽ đồ thị.
Tìm giao điểm của hai đường thẳng: Giải hệ phương trình bậc nhất hai ẩn để tìm tọa độ giao điểm.
Giải bài toán thực tế: Đổi các đại lượng trong bài toán thành các biến số, lập phương trình và giải.

Mẹo học tốt Toán 9 chương Hàm số bậc nhất

Để học tốt chương Hàm số bậc nhất, các em học sinh cần:

Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất của hàm số bậc nhất.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
Sử dụng các công cụ hỗ trợ: Sử dụng máy tính bỏ túi, phần mềm vẽ đồ thị để kiểm tra kết quả.
Hỏi thầy cô, bạn bè: Khi gặp khó khăn, đừng ngần ngại hỏi thầy cô, bạn bè để được giúp đỡ.

Bài tập luyện tập thêm

Để củng cố kiến thức, các em có thể tự giải các bài tập sau:

Bài 5 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2
Bài 6 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2
Các bài tập tương tự trong sách giáo khoa và các nguồn tài liệu khác.

Kết luận

Bài 4 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.