Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp cho các em đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài tập này ngay nhé!
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD tại F. Chứng minh ABEF và DCEF là hai tứ giác nội tiếp.
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD tại F. Chứng minh ABEF và DCEF là hai tứ giác nội tiếp.
Phương pháp giải - Xem chi tiết
Chứng minh tam giác ABE và tam giác AFE nội tiếp đường tròn đường kính AE.
Từ đó suy ra ABEF nội tiếp đường tròn. Chứng minh tương tự với DCEF.
Lời giải chi tiết
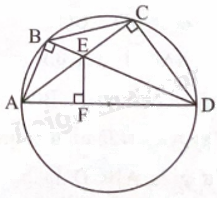
Ta có \(\widehat {ABE} = {90^o}\) (góc nội tiếp chắn nửa đường tròn); \(\widehat {AFE} = {90^o}\)(gt).
Tam giác ABE vuông tại B và tam giác AFE vuông tại F cùng nội tiếp đường tròn đường kính AE. Do đó, tứ giác ABEF nội tiếp đường tròn đường kính AE.
Chứng minh tương tự, ta có tứ giác DCEF nội tiếp đường tròn đường kính DE.
Bài 7 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song, vuông góc.
Bài 7 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng câu hỏi nhỏ:
Hệ số góc của đường thẳng y = ax + b là a. Trong trường hợp này, a = 2. Vậy hệ số góc của đường thẳng y = 2x + 3 là 2.
Hai đường thẳng song song khi và chỉ khi hệ số góc của chúng bằng nhau. Do đó, ta có phương trình:
m - 1 = 3
Giải phương trình, ta được m = 4.
Hai đường thẳng vuông góc khi và chỉ khi tích hệ số góc của chúng bằng -1. Do đó, ta có phương trình:
(2m + 1) * (-1) = -1
Giải phương trình, ta được m = 0.
Phương trình đường thẳng có dạng y = ax + b. Thay a = -1 và tọa độ điểm A(1; 2) vào phương trình, ta được:
2 = -1 * 1 + b
Giải phương trình, ta được b = 3.
Vậy phương trình đường thẳng cần tìm là y = -x + 3.
Khi giải các bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em đã hiểu rõ hơn về cách giải bài 7 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!