Giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.

Cho biết (soversetfrown{AB}=soversetfrown{BC}=soversetfrown{CA}) và OB = R. Độ dài cạnh BC là: A. (Rsqrt 3 ) B. (frac{{Rsqrt 3 }}{2}) C. (Rsqrt 2 ) D. (frac{{Rsqrt 3 }}{3})

Đề bài

Cho biết \(sđ\overset\frown{AB}=sđ\overset\frown{BC}=sđ\overset\frown{CA}\) và OB = R. Độ dài cạnh BC là:

A. \(R\sqrt 3 \)

B. \(\frac{{R\sqrt 3 }}{2}\)

C. \(R\sqrt 2 \)

D. \(\frac{{R\sqrt 3 }}{3}\)

Giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 1

Phương pháp giải - Xem chi tiết Giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 2

Dựa vào: Góc ở tâm bằng số đo cung cùng chắn một cung.

Lời giải chi tiết

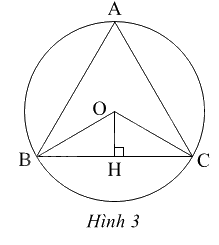
Ta có \(sđ\overset\frown{AB}=sđ\overset\frown{BC}=sđ\overset\frown{CA}=\frac{{{360}^{o}}}{3}={{120}^{o}}\) suy ra \(\widehat {BOC} = {120^o}\) (góc ở tâm bằng số đo cung cùng chắn một cung).

Mặt khác \(\Delta BOH = \Delta COH(g.c.g)\) suy ra \(\widehat {BOH} = \widehat {COH} = \frac{{\widehat {BOC}}}{2} = \frac{{{{120}^o}}}{2} = {60^o}.\)

Xét tam giác vuông BOH, ta có: BH = sin\(\widehat {BOH}\). R = sin 60^o .R = \(\frac{{\sqrt 3 R}}{2}\)

Vậy BC = BH + HC = 2BH = 2. \(\frac{{\sqrt 3 R}}{2}\)= \(R\sqrt 3 \).

Chọn đáp án A.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 đặc sắc thuộc chuyên mục giải sgk toán 9 trên nền tảng môn toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1: Tổng quan

Bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình đại số, tập trung vào việc giải phương trình bậc hai một ẩn. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về công thức nghiệm, định lý Vi-et và các phương pháp giải phương trình bậc hai để tìm ra nghiệm của phương trình.

Nội dung bài tập

Bài 3 thường bao gồm một số phương trình bậc hai khác nhau, có thể ở dạng tổng quát ax² + bx + c = 0 hoặc đã được biến đổi về dạng đơn giản hơn. Học sinh cần xác định đúng các hệ số a, b, c và lựa chọn phương pháp giải phù hợp.

Phương pháp giải phương trình bậc hai

Có nhiều phương pháp để giải phương trình bậc hai, bao gồm:

Sử dụng công thức nghiệm: Đây là phương pháp phổ biến nhất, áp dụng cho mọi phương trình bậc hai. Công thức nghiệm được tính như sau:

x_1,2 = (-b ± √(b² - 4ac)) / 2a

Sử dụng định lý Vi-et: Định lý Vi-et cho phép tìm mối liên hệ giữa nghiệm của phương trình và các hệ số a, b, c.
Phân tích thành nhân tử: Nếu phương trình có thể phân tích thành nhân tử, việc tìm nghiệm sẽ trở nên dễ dàng hơn.
Hoàn thiện bình phương: Phương pháp này giúp biến đổi phương trình về dạng (x + m)² = n, từ đó dễ dàng tìm ra nghiệm.

Hướng dẫn giải chi tiết bài 3 trang 98

Để giúp bạn hiểu rõ hơn về cách giải bài 3 trang 98, chúng tôi sẽ trình bày lời giải chi tiết cho từng phương trình:

Ví dụ 1: Giải phương trình 2x² - 5x + 2 = 0

Bước 1: Xác định hệ số: a = 2, b = -5, c = 2

Bước 2: Tính delta: Δ = b² - 4ac = (-5)² - 4 * 2 * 2 = 25 - 16 = 9

Bước 3: Tính nghiệm: Vì Δ > 0, phương trình có hai nghiệm phân biệt:

x₁ = (-(-5) + √9) / (2 * 2) = (5 + 3) / 4 = 2

x₂ = (-(-5) - √9) / (2 * 2) = (5 - 3) / 4 = 0.5

Kết luận: Phương trình có hai nghiệm x₁ = 2 và x₂ = 0.5

Ví dụ 2: Giải phương trình x² - 4x + 4 = 0

Bước 1: Xác định hệ số: a = 1, b = -4, c = 4

Bước 2: Tính delta: Δ = b² - 4ac = (-4)² - 4 * 1 * 4 = 16 - 16 = 0

Bước 3: Tính nghiệm: Vì Δ = 0, phương trình có nghiệm kép:

x₁ = x₂ = -b / (2a) = -(-4) / (2 * 1) = 2

Kết luận: Phương trình có nghiệm kép x₁ = x₂ = 2

Lưu ý khi giải phương trình bậc hai

Luôn kiểm tra kỹ các hệ số a, b, c trước khi áp dụng công thức nghiệm.
Chú ý đến dấu của delta để xác định số nghiệm của phương trình.
Nếu delta âm, phương trình vô nghiệm.
Nếu delta bằng 0, phương trình có nghiệm kép.
Nếu delta dương, phương trình có hai nghiệm phân biệt.

Bài tập luyện tập

Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:

Giải phương trình 3x² + 7x - 2 = 0
Giải phương trình x² - 6x + 9 = 0
Giải phương trình 5x² + x + 1 = 0

Kết luận

Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!